起因

最近双十一，各大电商平台造势，宣传自己当天平台销售额，而有个网友爆料天猫销售额造假，因为自己在几个月前就已经成功预测了今年双十一的销售额，并给出了自己的模型参数（公式）。
2019年11月12日网民认为尹立庆神推算的微博

实验

首先，我们按照楼主的思路做一个的实验。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt 
import numpy as np


tm_2009_2019 =  [0.50, 9.36, 52.00, 191.00, 350.00, 571.00, 912.00, 1207.00, 1682.69, 2135.00]
year = list(range(2009, 2019))
year = list(map(lambda x: x-2009, year))


def sse(y_pre, y_true):
    se = (y_pre - y_true) ** 2
    return se.sum()

def ssr(y_pre, y_true):
    sr = (y_pre - y_true.mean()) ** 2
    return sr.sum()

def R(y_pre, y_true):
    se = sse(y_pre, y_true) 
    sr = ssr(y_pre, y_true)
    return sr/(se+sr)

def build_model(x, y, degree=3):
    x = np.array(x).reshape(-1,1)
    y = np.array(y).reshape(-1,1)
    pf = PolynomialFeatures(degree=degree)
    X = pf.fit_transform(x)
    linear_reg = LinearRegression()
    linear_reg.fit(X, y)
    y_pre = linear_reg.predict(X)
    print('R is: ', R(y_pre, y))
    return linear_reg, pf

def predict(model, pf, test_x):
    test_X = pf.transform(np.array(test_x).reshape(-1,1))
    return model.predict(test_X)

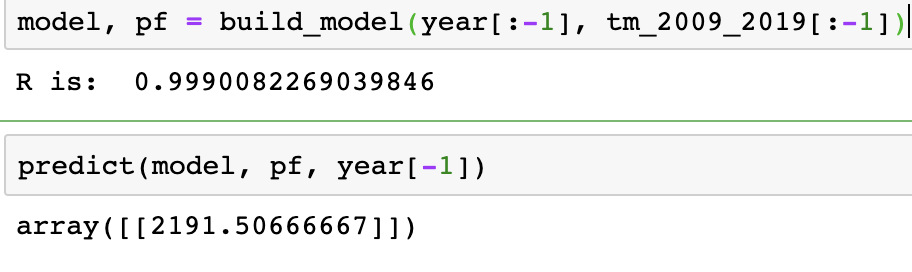
可以看到，此时的拟合优度R高达0.999，而预测今年的值为2689，确实也与今年的实际值2684基本吻合，所以网友认定自己成功的发现了天猫双十一的销售额”模型”。
接下来，我们做几个不一样的实验来看看其结果。
实验1
这次我们将数据修改一下：将第三年和倒数第三年的数据都减少10%，其他参数不变，看看模型效果。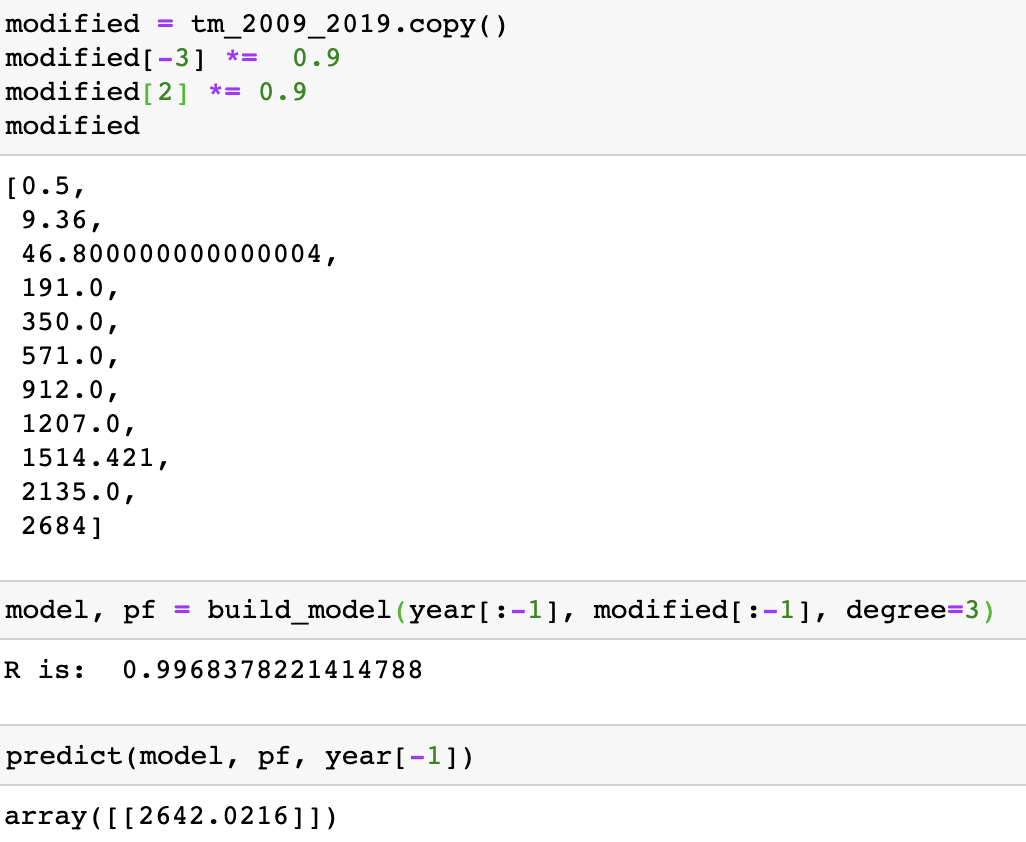

拟合优度0.996，预测值为2642，与今年实际值也基本吻合。

实验2
这次我们不再使用全部数据，而只用2013-2018这六年的数据，其他不变，来看看我们的模型效果如何。

拟合优度也高达0.997，而且预测值2672也与今年的实际值基本吻合。

实验3
这次我们不再使用三次，而换为二次线性方程来拟合，仍然使用原始的十年数据。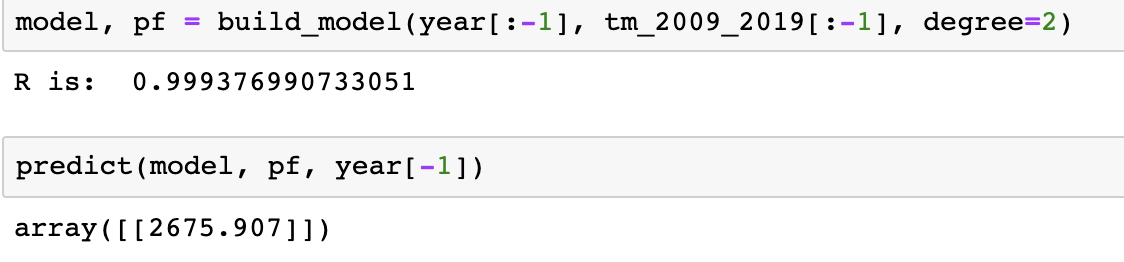

拟合优度0.999，预测值为2675，与今年的实际值也基本吻合。

实验小结

实验1与实验2说明，对样本做一定处理后，对模型最终的拟合影响不大，原因是在求解模型时，通常我们使用的loss是欧式距离（最小二乘估计），整体的
loss是对所有样本拟合loss的和，所以模型在拟合时会更”关注”值大的样本，而前几年的值与后几年相比差距一个数量级，所以不使用值很小的样本对模型
影响不大。而实际建模时，对于样本范围跨度很大的特征，通常我们都需要平滑而不是直接使用原始值。
实验3我们使用了一个参数更小的模型，$f(x) = A + Bx + Cx^2$, 而原始模型使用三次拟合，$F(x) = A + bx + Cx^2 + Dx^3$, 两个模型明显是
不同的，但是却都能拟合数据，这是因为这些模型都过拟合了，也就是对于一批离散点，总是能找到一个函数F，可以非常好的拟合他，这也是冯诺伊曼的那
个笑话：四个参数画大象，五个参数鼻子晃。

什么是过拟合

在这个问题上，一些网友说，这个模型肯定是有效的而不是过拟合，因为他”完美预测”了今年的真实值，模型如果只是单纯的在之前的数据上很好的拟合，而不能成功预测今年的真实值，这才是过拟合，现在模型成功预测了今年的值，所以现在的模型是有效的，不存在过拟合。
为了说明这个问题，我们来简单讨论一下，什么是过拟合，是不是成功预测了就不存在过拟合。
首先，我们来简单说明一下，一个模型的误差分为两部分，一部分是因为模型对训练数据拟合的不好带来的误差，这部分我们称为偏差；而由于抽样过程中，抽出的训练样本与整体样本分布不同引起的误差，我们称为方差。而当我们抽样时是有偏的，即抽样与整体样本分布不同，而我们的模型又对训练数据拟合的非常好，此时的模型我们就称之为过拟合，即他虽然对样本拟合的很好，但是由于样本与整体分布不同，导致模型在泛化时性能并不好，通常比在训练集上要差很多，因为毕竟模型拟合的是一个与整体不同分布的数据集，拟合的越好，泛化越差。
那当模型在新的样本上预测对时，是不是就不能说他过拟合呢？其实也不尽然，本质上过拟合只与你的整个过程有关，至于最终的模型在新样本上预测的准不准，并不能说明这个模型是否过拟合，毕竟瞎猫还能碰上死耗子，模型拟合的数据集虽然与整体分布不同，但是毕竟也是整体数据的一部分，预测准
一部分数据也正常，毕竟我们说过拟合的泛化性能低，但不是说他泛化低到全错。
所以对应天猫的这个案例，总的来说天猫的销售额是一个复杂的业务场景最终带来的结果，而仅仅用最终的销售额来进行模型，忽略各种业务策略的影响因素，显然与业务的真实分布相去甚远，不然也不用投入这么多人力物力，直接等着新的一年到来就好了，因为你不管怎么调整，最终的结果都是”模型”定好的。

通俗的解释

当我用上面这些论述来解释时，同事告诉我：”我不懂数学不懂机器学习，我就知道他的模型预测对了，都预测对了，你怎么能说他不准呢，还过拟合，过拟合不是预测不对才叫过拟合吗？” 这时我会换一个场景，”假如现在有个人，通过之前的十期双色球，预测对了这期对双色球，那你要不要用他的模型，重金投入买下一期的双色球呢？”

知识诅咒

最近学到了一个新的概念：知识的诅咒，其含义是当你知道了一件事后，你就无法想象自己是不知道这件事的。而造成这种现象的根本原因是信息的不对等。在我最初给人解释天猫销售额事件时，对面总是听不太懂我在说什么，我也搞不清楚为什么我说的这么简单直白，他会听不懂，当看到知识诅咒这个概念后，这个问题就有了答案了。

关于头图

摄于故宫

Buy me a coffee

如果觉得这篇文章不错，对你有帮助，欢迎打赏一杯蜜雪冰城。