
分词算法综述
分词现状
NLP的底层任务由易到难大致可以分为词法分析、句法分析和语义分析。分词是词法分析(还包括词性标注和命名实体识别)中最基本的任务,可以说既简单又复杂。说简单是因为分词的算法研究已经很成熟了,大部分的准确率都可以达到95%以上,说复杂是因为剩下的5%很难有突破,主要因为三点:
- 粒度,不同应用对粒度的要求不一样,比如“苹果手机”可以是一个词也可以是两个词。
- 歧义,比如“下雨天留人天留我不留”。
- 未登录词,比如“skrrr”、“打call”等新兴词语。
分词算法根据其核心思想主要分为两种,第一种是基于字典的分词,先把句子按照字典切分成词,再寻找词的最佳组合方式;第二种是基于字的分词,即由字构词,先把句子分成一个个字,再将字组合成词,寻找最优的切分策略,同时也可以转化成序列标注问题。归根结底,上述两种方法都可以归结为在图或者概率图上寻找最短路径的问题。
- 未登录词,比如“skrrr”、“打call”等新兴词语。
基于词典的分词
最大匹配分词算法
最大匹配分词寻找最优组合的方式是将匹配到的最长词组合在一起。主要的思路是先将词典构造成一棵Trie树,也称为字典树。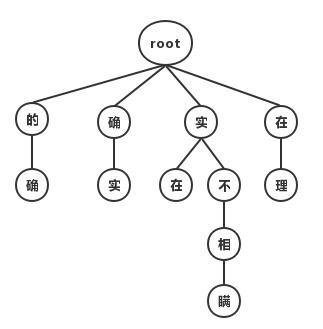
Trie树由词的公共前缀构成节点,降低存储空间同时提升查找效率。最大匹配分词将句子与Trie树进行匹配,在匹配到根节点后由下一个字重新开始查找。最大匹配又分为前向匹配和后向匹配算法,如上图中,对语句“他说的确实在理”,前向最大匹配的结果“他/说/的确/实在/理,而反向最大匹配结果”他/说/的/确实/在理“。通过词典最大匹配时间效率虽然高,但是效果很差,实际一般很少使用这种方法。
最短路径分词算法
最短路径分词算法首先将一句话中的所有词匹配出来(基于词典),构成词图(有向无环图DAG),然后寻找从起始点到终点的最短路径作为最佳组合方式。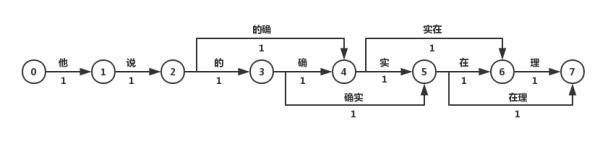
图中所有词的权重都是相等的,所以每条边的权重都是1.
DAG图的最短路径问题,可以描述为 在无向图 $G=(V,E)$ 中,假设每条边 $E[i]$ 的长度为 $w[i]$,找到由顶点 V0 到其余各点的最短路径(单源最短路径)。假设源点为S,节点集合为V,终点为E。对于最短路径$P(S,E)$中的中间节点,其源点到其的最短路径也在$P9SE)$内。即:假如$S->A->B->C->E$是最短路径,那$S->A->B$一定是S到B的最短路径,否则,将会存在一点F,使得$d(S->F->B)<d(S->A->B)$,而最短路径$P1(S,E)=S->F->B->C->E$将比$P(S,E)$短,从而与假设矛盾。因此,求解DAG可以利用最优子结构,通过贪心或者动态规划来求解。
Dijkstra算法
Dijkstra算法本质是贪心算法,每一步求解最短路径节点,然后递推更新源节点到其他节点的距离。
算法步骤:
- a.初始时,S只包含源点,即$S={v}$,v的距离为0。U包含除v外的其他顶点,即:U={其余顶点},若v与U中顶点u有边,则$<u,v>$正常有权值,若u不是v的出边邻接点,则$<u,v>$权值为∞。
- b.从U中选取一个距离v最小的顶点k,把k,加入S中(该选定的距离就是v到k的最短路径长度)。
- c.以k为新考虑的中间点,修改U中各顶点的距离;若从源点v到顶点u的距离(经过顶点k)比原来距离(不经过顶点k)短,则修改顶点u的距离值,修改后的距离值的顶点k的距离加上边上的权。
- d.重复步骤b和c直到所有顶点都包含在S中。
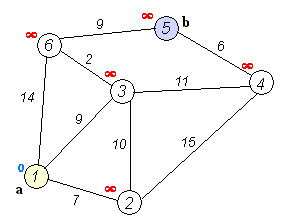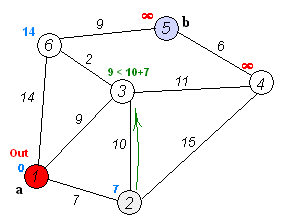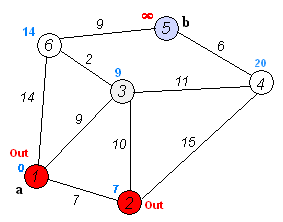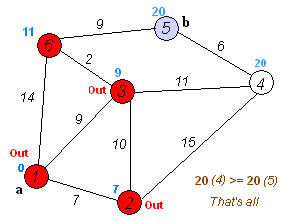
Dijkstra算法的结果为”他/说/的/确实/在理“,可见最短路径分词可以解决大部分问题,但是当最短路径存在多条时,Dijkstra只保存一条,这种策略即缺乏理论依据也对其他路径不公平。
N-最短路径分词算法
N-最短路径分词是对Dijkstra算法的扩展,他在每一步都保存最短的N条路径(beam search),同时记录当前节点的前驱,最后求得最优解时回溯得到最短路径,该算法结果优于Dijkstra,但是时间与空间复杂度上更大。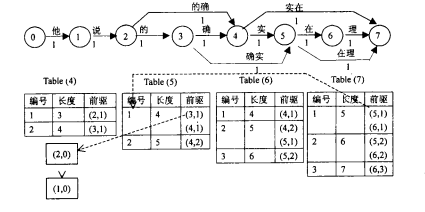
基于n-gram model的分词算法
前文中边的权重都是1,但实际中不同的词出现的频率/概率不同,其成词的概率也就相应不同,因此将求解词图最短路径的问题转化为求解最大概率路径问题。即将句子切分为”最有可能的词的组合“。而计算词出现的概率,就需要语料对”语言“进行统计建模。
语言模型是对一句话出现的概率进行建模,根据条件概率:
p(他说的确实在理) = p(他)p(说|他)p(的|他说)…p(理|他说的确实在)
上述计算过于庞大,一般我们采用n-gram来近似,如2-gram。
然后我们将语言模型得到的概率分布应用到词图,可以得到词图的概率图 :
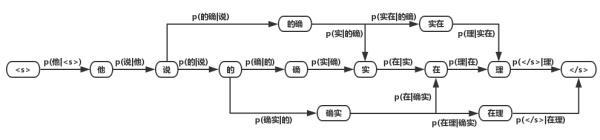
利用上面两种求解DAG最短路径的方法进行求解即可。
基于字的分词
与基于词典的分词不同,基于字的分词事先不对句子进行词匹配,而是将分词看成是给句子中的每个字打上标签的序列标注问题,可以看成是对每个字的分类问题。 比如通过4标签来进行标注(single,单字成词;begin,多字词的开头;middle,三字以上词语的中间部分;end,多字词的结尾。均只取第一个字母。),这样,“为人民服务”就可以标注为“sbebe”了。 4标注不是唯一的标注方式,类似地还有6标注,理论上来说,标注越多会越精细,理论上来说效果也越好,但标注太多也可能存在样本不足的问题,一般常用的就是4标注和6标注。
HMM模型
HMM模型认为在解决序列标注问题时,存在两种序列,一种是观测序列,是人显性观察到的句子,而标签是隐状态序列,即观测状态为X,隐藏状态序列是Y,因果关系是Y->X.
我们用$λ=λ1λ2…λn$表示输入的句子,用$o= o1o2…on$表示对应的label,那最优的输出是什么呢?从概率的角度,我们希望下面的条件概率最大:
$max P(o∣λ)=max P(o1o2…on∣λ1λ2…λn)$
也就是,o有很多种可能,但是最优的是o应该是概率最大的o。而上式的概率是关于2n个变量的条件概率,而且不同的输入有不同的n,精确计算基本不太可能,所以,我们为了简化问题,先提出第一个假设:输出只与对应的输入有关。于是,上式就可以简化为:
$maxP(o∣λ)=max P(o1∣λ1)P(o2∣λ2)…P(on∣λn)$
现在,上式的求解就简单多了,只要让每个**P(ok|λk)**最大,即可得到最大的$P(o|λ)$.
上面的方案是一个简化方案,但是完全没有考虑上下文,这样会出现很多不合理的结果,比如按照我们4标注方法,b后只能接m或者e,而上述方案不考虑上下文,就可能出现bb\bs等错误结果。这些都是不合理的结果。而产生这种结果的原因是我们没有考虑label之间的关系,所以,我们需要换个角度,反过来考虑这个问题。
首先,利用贝叶斯公式: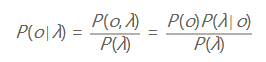
由于λ是给定的输入,那么P(λ)就是常数,我们忽略他。现在,最大化$P(o|λ)~P(o)P(λ|o)$.此时,我们的模型是考虑了输出之间的关系$P(o)$,就可以避免一些不合理的情况的出现。
$P(o)P(λ|o)=P(o1o2…on)P(λ1λ2…λn|o1o2…on)$
根据我们第一个假设,我们得到:
$P(λ|o)=P(λ1|o1)P(λ2|o2)…P(λn|on)$
对于$P(o)$,有
$P(o) = P(o1)P(o2|o1)…P(on|o1o2..on-1)$
此时,我们提出第二个假设:输出状态只与前一个状态有关。
$P(o) = P(o1)P(o2|o1)…P(on|on-1)$
此时,
$P(o|λ)~P(λ1|o1)P(o2|o1)P(λ2|o2)P(o3|o2)…P(on|on-1)P(λn|on)$
其中,$P(λk|ok)$称为发射概率,$P(on|on-1)$称为转移概率。对于不合理的输出序列,如bb,我们可以通过设置其状态转移概率为0来避开。
接下来的HMM模型的训练,就是如何求解发射概率与转移概率了。
学习训练主要有极大似然估计和 Baum-Welch(前向后向)两种算法,通常用极大似然估计。如果有一批标注好的语料,这俩个概率的估计就非常简单了,但通常我们没有大批标注好的语料,我们可以通过词典和未标注的语料来估计,如果没有语料,我们可以通过词典来估计发射概率,状态转移概率人为给一个。
得到了发射概率和转移概率,此时就是计算给定输入的最大概率的输出序列。设输入序列长度为L, 状态(label)有n种,则有 $n^L$种可能的排列方式,此时计算最大概率的复杂度为$O(Ln^L)$,这个量太大了,不可取,于是,维特比算法登场了。
维特比算法
维特比算法是HMM,CRF中的经典解码算法,其核心是通过DP思想,在每个时间点的每个label上存储到该位置的最大概率,将计算复杂度降低为 $O(L^2n)$。其流程图如下:
算法流可能不够直观,下面来通过一个例子来更好的理解。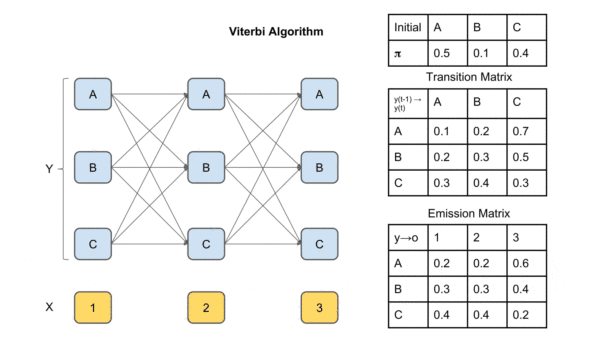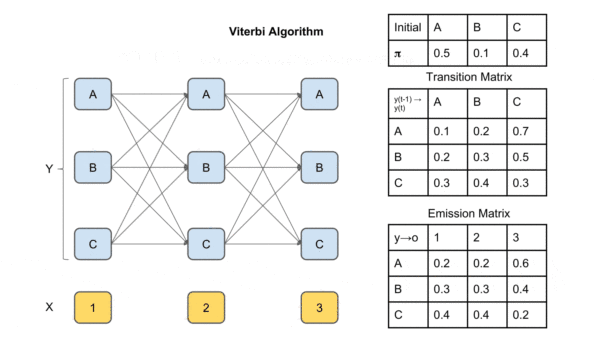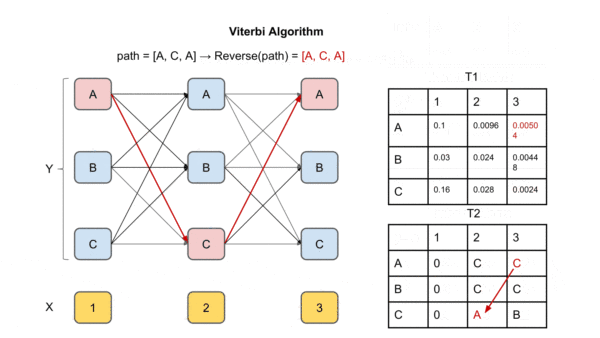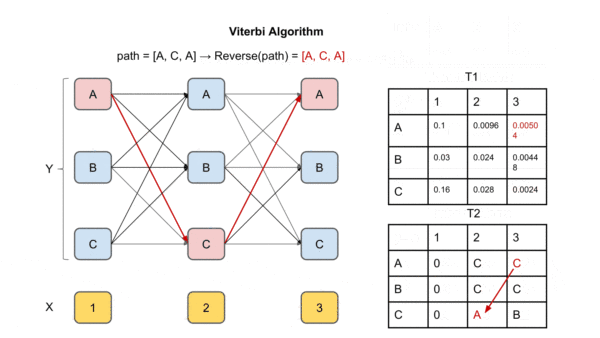
图中X是观察序列(输入序列),Y是标签矩阵。T1为每个时间点每个label的最大概率,
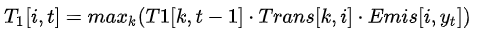
T2为到达该时间点该label最大概率的前驱label(上个时间点上)
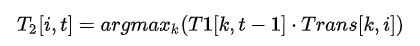
到达最后一个时间点后,求解最大概率对应的label,然后通过T2回溯,将对应前驱节点加入path直到到达起始时间点,得到的path即为最优解的逆序,反转即可得到最优路径(最大概率的输出标签序列)。
CRF
CRF可以看作一个无向图模型,对于给定的标注序列Y和观测序列X,对条件概率$P(Y|X)$进行建模。首先,我们讨论一下有向图与无向图概率模型。
有向图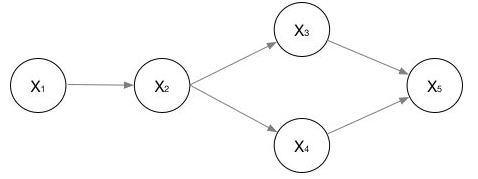
上图是一个广义的有向图,他们的联合概率数学表示为: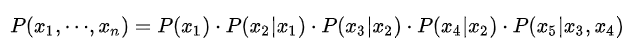
无向图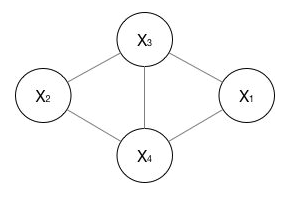
上图是一个广义的无向图,而求解时,需要将其分解为若干个“小团”的联合概率的乘积,而每个小团必须是“最大团”(子图里任意两个节点是相连的,且没有其他节点能加入使他成为跟大的团),则有:
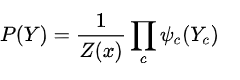
其中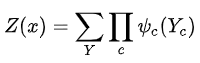
用来归一化,将结果转化为概率。
上图的无向图的联合概率表示为: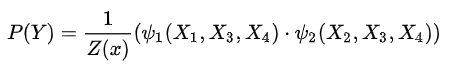
其中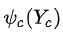
是最大团C上随机变量的联合概率,形式一般取指数函数: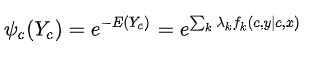
上式也叫势函数。
无向图的联合概率分布在因子分解下表示为: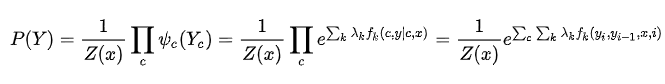
上式中化简为各个团的联合概率的乘积由 Hammersly-Clifford law保证。
广义的CRF的定义是: 满足 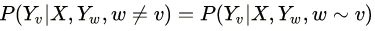
的马尔科夫随机场叫做条件随机场(CRF),一般我们说的是线性链条件随机场,定义为:
$P(Y|X) = P(Yv|X, Yv-1, Yv+1)$
下面来看看我们在做序列建模时,对应的图结构。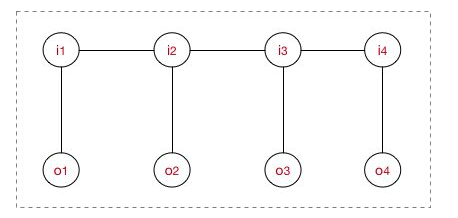
上图是一个序列建模(线性链CRF)时,对应结构示意图,为了求解上图中的概率,我们需要对上图进行因子分解,分解成若干个“最大团”,而上图结构中,每个“最大团”都是由一对(Ii~Oi)组成,即每个“最大团”C与位置I对应,c=i,而且线性链CRF满足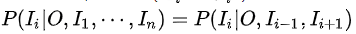
,我们带入无向图的联合概率分布的因子分解,对应的CRF建模公式为: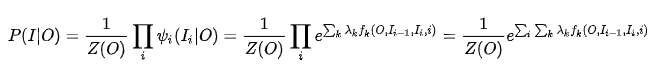
公式内i是对应当前节点对应位置;k表示第几个特征函数,每个特征函数对应一个特征权重$λ_k$, $Z(o)$的作用是归一化为概率。
对于特征函数,我们可以定义两类特征函数:转移特征和状态特征,我们可以将上式展开为: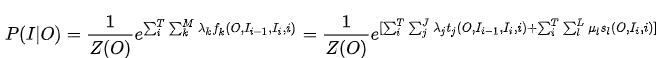
其中$tj$为转移特征,对应权重为$λj$, $sl$为状态特征,对应权重为$ul$。一般我们不分开看,将对应特征函数统一起来。
CRF学习过程中,需要提前定义特征函数,然后根据样本来学习对应特征的权重,所以CRF中比较困难的点在于需要定义大量的特征函数,特征函数的质量直接影响最后的模型质量。
下面借一个列子(CRF++)来说明一下:
首先,我们会定义相应的标签数据:
1 | "tags": [ |
然后我们会定义特征模版,通过特征模版,会帮助我们产生相应的特征函数:
1 | # Unigram |
其中,我们定义了7个U系列模板(Unigram)和一个B系列(Bigram)模板,其中U00:%x[-2,0]代表U系列,索引为00,对应特征是当前位置的左侧第二个位置(-2)token和当前位置的token,最后的B代表只有一个B系列特征,即只有当前位置的前一个位置的输出token(标签)与当前位置的token(标签)组成的Bigram一个特征(转移概率)。接下来看看对应学习后输出:
1 | "feature_func_weight":{ |
上面这个代表的是什么呢?就是对应第“006”的“U”系列特征是“等”字时,对应五个(BEMOS)对应得分,通过模板,会对每个字都生成对应的6个特征,每个特征都有对应的特征函数权重。
HMM与CRF的关系是什么?
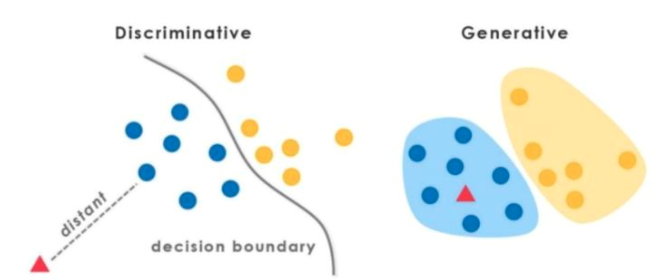
在介绍两者区别之前,我们先来讨论一下机器学习中的两种不同的模型:生成式模型与判别式模型。
在监督学习下,模型可以分为判别模型和生成模型。判别模型通过features对labels刻画边界,即他直接对P(X|Y)进行建模;而生成模型通过训练样本,确定数据的整体分布情况,即他直接对P(X,Y).
我们的目标是对$P(o|λ)$进行求解,在HMM中,我们通过贝叶斯公式,将问题转化为:
分母是常数,被我们忽略了,本质上是对分子进行建模,即对$P(o,λ)$进行建模,所以是一个生成模型。而CRF,直接对$P(o|λ)$进行建模,是一个判别模型。
除此之外,CRF可以解决HMM能解决的一切问题,还能解决许多HMM解决不了的问题。为了说明这一点,我们来看看他们的数学表达形式。HMM模型的数学表达为: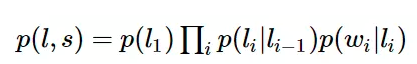
如果我们将HMM模型取对数,可以得到: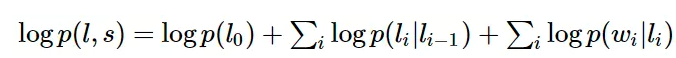
而CRF的未归一化的log形式(特征函数)的数学表达为: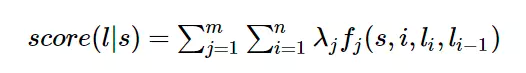
如果将HMM中的log形式看作是CRF中的特征权重,则两者具有相同的形式,即每一个HMM都对应某一个形式的CRF。
维特比算法与两者(HMM/CRF)的关系是什么?
维特比算法是一类问题的解法,而不是固定只与HMM\CRF搭配。CRF与HMM都有两个过程,一个是学习阶段,一个是解码阶段。学习阶段确定模型参数,解码阶段求解最大概率路径。解码过程中,HMM与CRF(线性链CRF)从模型定义上看,每个位置的得分都是依赖前一个位置的信息(标签信息),所以整体是一个递推过程,而这个过程在求解最大概率路径时,如果是穷举,在上文也讨论了,复杂度为$O(L*n**L)$,而维特比算法将复杂度降低为$O(L**2*n)$。所以维特比算法是刚好适用于HMM/CRF解码过程的一种算法。
神经网络分词算法
对于序列建模这类问题,RNN有着天然的优势,可以很方便的处理变长输入和序列输入,目前对于序列标注问题,公认效果最好的模型是BiLSTM+CRF,对应的模型结构为: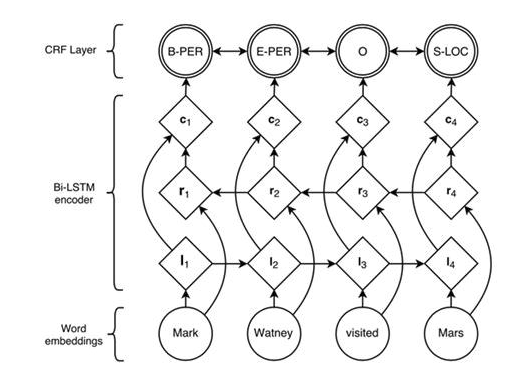
相比于其他模型,BiLSTM可以学习到上下文相关信息,可以很好的解决序列输入问题,但BiLSTM只学习到了输入的上下文信息,对应标注的上下文信息却完全没有用到,所以正如HMM中我们讨论的一样,会出现很多不合理的标签序列,如$b\b\b$这种,所以,在后面接一个CRF来避免这种情况的出现。
参考
https://www.cnblogs.com/biyeymyhjob/archive/2012/07/31/2615833.html
https://baike.baidu.com/item/%E8%BF%AA%E6%9D%B0%E6%96%AF%E7%89%B9%E6%8B%89%E7%AE%97%E6%B3%95/4049057?fr=aladdin#reference-[1]-1712262-wrap
https://wenku.baidu.com/view/da6e0921af45b307e8719702.html
https://zhuanlan.zhihu.com/p/63087935
https://www.cnblogs.com/pinard/p/7048333.html
https://www.zhihu.com/question/35866596/answer/236886066
https://www.cnblogs.com/pinard/p/7048333.html
https://blog.echen.me/2012/01/03/introduction-to-conditional-random-fields/
https://www.zhihu.com/question/20279019
http://taku910.github.io/crfpp/
关于头图
摄于北京欢乐谷
