LLM Inference串讲

小蛋子

2023-03-10

本文主要概述一下当前LLM 是如何生成文本及为什么对应的资源（cost/latency)与prompt 和completion 都有关系。

generation

上一篇我们讲了为了解决自然语言问题，我们引入了统计语言模型：$S$ 表示一连串特定顺序排列的词$w_1$, $w_2$, …, $w_n$,其中$n$ 是序列的长度，则$S$ 出现的概率$P(S)=P(w_1,w_2,…w_n)$. 通过序列的概率，来判断对应句子是否合理。而这个概率$P(S)$ 很难估算，所以我们将其转化一下。首先，利用条件概率公式将其展开:
$$
P(S)=P(w_1,w_2,…,w_n)=P(w_1)∗P(w_2∣w_1)∗P(w_3∣w_1,w_2)∗…∗P(w_n∣w_1,w_2,…,w_{n−1})
$$
即：
$$
P(w_1^n)=\prodP(w_i∣w_1^{i−1})
$$
然后用深度神经网络，对$P(w_i|w_1^{i-1})$ 进行建模，即：
$$
P(w_i|w_1^{i-1}) = g(w_1^{i-1})
$$

其中$g$ 是深度神经网络，如MLP/RNN/Transformer 等。

文本生成的过程，即我们在已有的深度神经网络$g$ 下，生成（采样）合理句子（序列）的过程。其中$g$ 能生成给定context $C$ 时下一个时刻对应的词表分布, 其中$C$ 是由$w_1$, $w_2$, …, $w_m$ 组成的序列。
目前我们训练$g$ 通常采用Teacher-Forcing 的方式：训练阶段，每个时刻$t$ 之前的label $y_{<t}$都是已知的，就像是老师讲课一样，将每一步的正确解题思路都告诉你，你只需要跟着老师的思路一步一步推导就能得到正确答案；然而在inference 阶段，我们是没法知道当前时刻之前的真实label 是什么的，所以需要将所有可能的序列的概率都求解出来，最后在所有可能性中选择概率最大的。如同考试时没了参考步骤，只能尝试多个思路，最后保留我们觉得”正确“的。

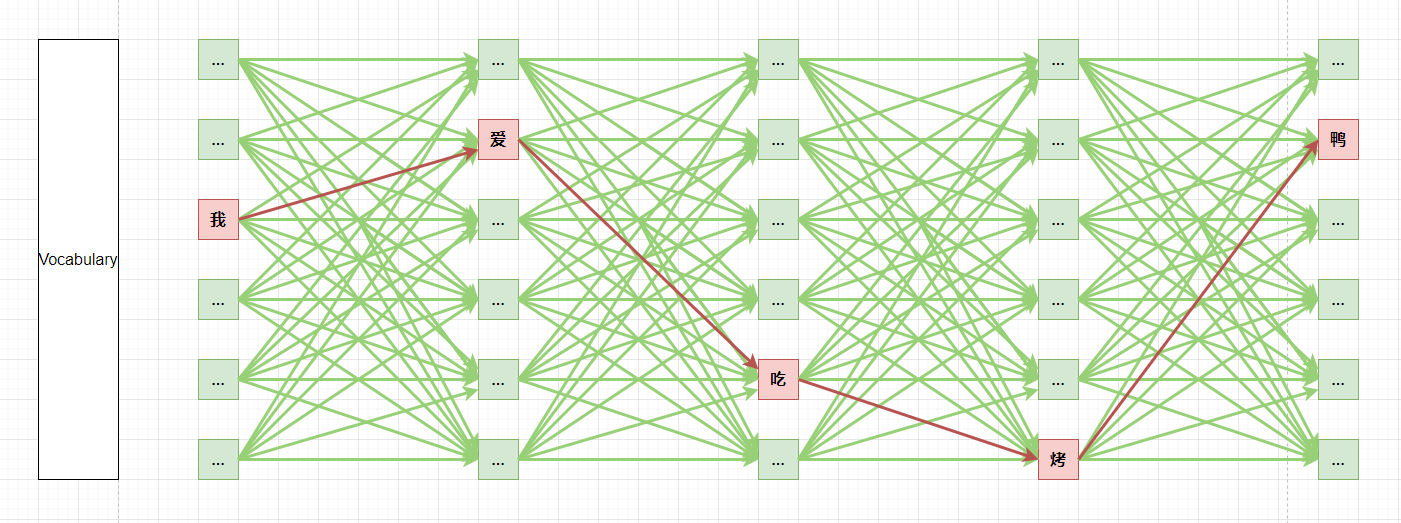
求解过程是一个求解最优路径问题，然而这个计算量太大了。假设我们的词表大小是$V$, 生成序列的长度为$k$, 每一个时刻都需要对所有状态（整个词表）进行计算，即使我们的词表只有五万个词，要生成五个token 也需要计算25万次，这个计算量实在是太大了。所以我们需要一些更高效的生成策略。

概率值$p$ 是一个范围在$0\sim 1$ ，多次连乘后会很快接近0，所以通常我们会将$max\prod p_i$ 转换为求$max \sum log(p_i)$

Greedy Search

Greedy search 的思路是：每次都选择概率最高的词作为最终采样结果，即: $w_t = argmax_wP(w|w_1^{t-1})$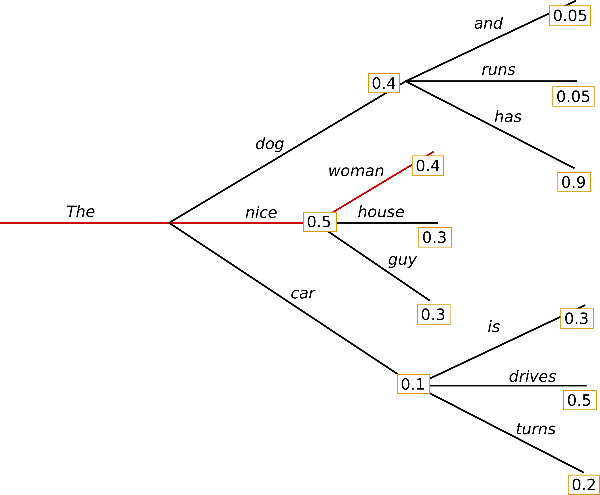

该方法是缺点也很明显：局部最优的最终结果很可能不是全局最优，由于每次都是选局部最优，这也扼杀了模型找到全局最优的可能性。如上图中Greedy search 的结果是(The, nice, woman),而全局最优是(The, dog, has) .除此之外，模型的生成结果也不够”丰富“，甚至会出现不停重复之前的内容。

Beam Search

”多一个选择，多一次机会“。为了缓解Greedy search 的问题，我们在每次选择时，不再只保留最高概率的一个，而是所有候选中保留概率最高的N 个(num_beams/beam_width) path。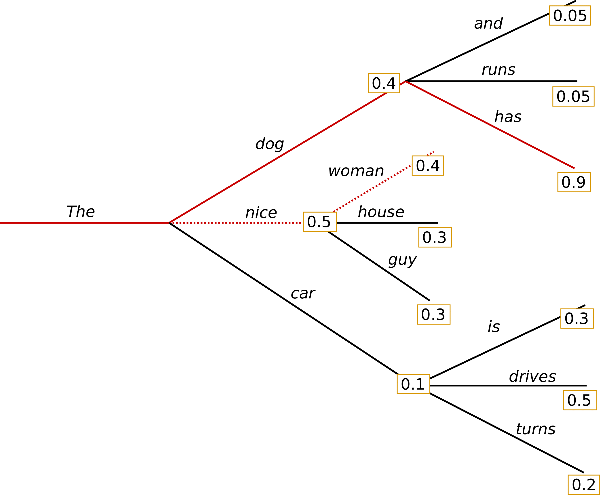

上图是num_beams=2 的示例：

第一步时，在(The, dog)/(The, nice)/(The car) 三个路径中选择概率最高的两条path:(The, nice), (The, dog)
第二步时，在(The, nice, wowan)/(The, nice, house)/(The, nice, guy)/(The, dog, and)/(The,dog,runs)/(The,dog,has) 中选择路径概率（单步概率连乘）最高的两条path:(The, dog, has), (The, nice, woman)
依此类推，直到满足终止采样.

此前Greedy Search 未找到的最优路径，此次通过Beam Search 找到了，但是依然无法保证每次都能找到全局最优。PS: num_beams =1 时，与Greedy Search 过程相同。

Sampling

以上两种方法都是确定性解码（deterministic），缺点就是不够丰富，不够”surprise“；为了让生成的内容更加的丰富多样有惊喜，我们可以采用另一种策略：采样（Sampling).

采样的基本思路是在概率分布上进行随机采样，选择一个作为下一个词$w_t$:
$$
w_t \sim P(w|w_1^{t-1})
$$
然而由于模型$g$ 距离真实的$P(w|w_1{t-1})$ 还是会有差距，直接按照$g$ 生成的”概率分布“采样风险太大，很容易走偏；一个折中的办法是控制候选集，在“低风险”范围内采样。
候选集的构造方式也有多个，常用的有topK/topP/beam-search.

topK

每次选择概率最大的K 个作为候选集，然后重新归一化，获取新的分布后进行采样。

对词表进行排序，选择概率最高的K 个；
对候选集中的K 个候选的概率值进行归一化，构造K 个候选对应的分布$\widetilde{P}$
从分布$\widetilde{P}$ 中采样一个词作为$w_t$

topP

topp sampling 又叫nucleus sampling,其思路是不在从通过保留最大的K 个作为候选，而是保留概率累计和范围$p$ 内的所有词作为候选集，候选集大小随着分布变化而动态调整。

对词表进行排序，从大到小进行排列
依照概率大小，依次将词加入候选集，直到新增的词进入候选集后，整个候选集内的概率累计和大于$p$ 停止；
对候选集内的词进行归一化，构造新的分布$\widetilde{P}$
从分布$\widetilde{P}$ 采样一个词作为$w_t$

topk 与topp 也可以一起使用，通常实现时是先进行topk，然后在topk 归一化后的候选集上进行topp 采样。

beam-search sampling

该方法是beam-search 的samling 版，其主要思路是：在每次选择时，不在直接选择所有候选中概率最高的num_beams 个，而是从中采样。

generate parameters

Temperature

通常模型的输出是一些值（logits)而不是分布（probability distribution),我们需要将其转换成分布，转换通常使用的是softmax 函数：
$$\frac{\exp(z_i)}{\sum_jexp(z_j)}$$

softmax 函数的特点是：

保持其原有的相对顺序;
累计和为1。

然而其缺点也明显：很容易扩大/缩小内部元素的差异（softmax 变 max/mean），如 [11, 12, 13 ] softmax 后为[0.0900, 0.2447, 0.6652], 这将导致最终我们采样后的结果不够丰富；而[0.01,0.02,0.03] softmax 后[0.3300, 0.3333, 0.3367],这将导致最终的采样方法是在随机采样，生成不合理的序列。为为了解决这个问题，我们需要有个办法调节，让softmax 后的分布进一步符合我们的预期，对应的办法就是增加参数$T$:
$$\frac{\exp(z_i/T)}{\sum_jexp(z_j/T)}$$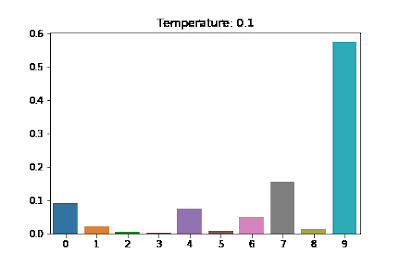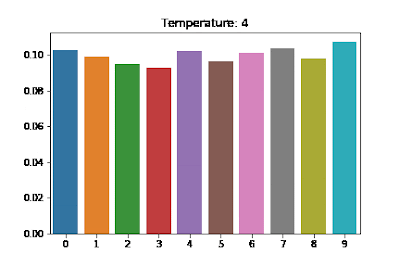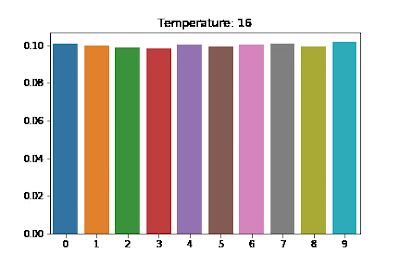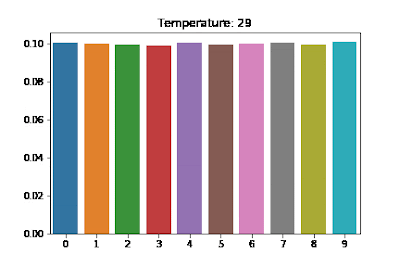

$T$ 越大，分布越趋近均匀分布(uniform distribution)，采样结果随机性越大，生成的序列是不合理句子的概率就越高；
$T$ 越小，分布越趋近与单点分布(one-point distribution)，采样结果越趋近保持一致。

* penalty

除了temperature 这种对整体分布进行修改外，还有些场景需要我们对特定的某些token 的分布进行修改，此时就诞生了各种penalty，如repetition_penalty/diversity_penalty等参数。注意：这里是对其分布乘以一个系数，其结果有可能并不改变其大小顺序。

强制/禁止特定token 的出现

一些场景下，我们要求更加苛刻：希望某些token 一定/永不出现，同理，此时将满足条件的token 的分布直接调整为100%/0%，如bad_words_ids/no_repeat_ngram_size/force_words_ids 等参数。

GPU

下面已A100-80G SXM 为例，了解一下GPU 的基本信息。

A100 specifications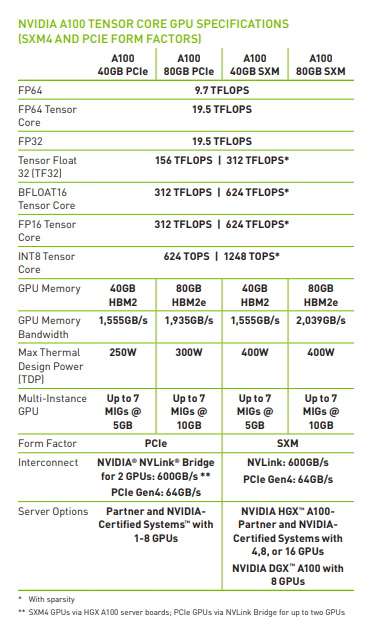

simplified view of the GPU architecture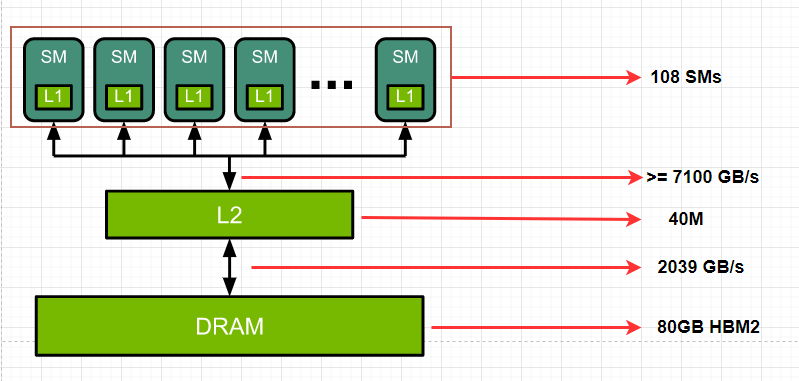

Multiply-add operations per clock per SM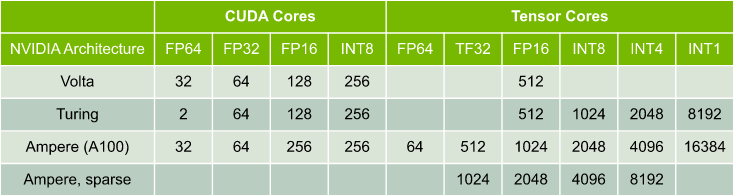

FP16 Tensor Core peak dense throughputs:
$$1024 (Tensor cores) \ast 108 (SMs) \ast 1.41 GHz (clock rate) \ast 2 (multiply-add) = 312 TFLOPS $$

performance

性能主要受限于三个因素：内存带宽(memory bandwidth)，计算带宽(math bandwidth), 延时(latency).

假设我们访问内存花费的时间为$T_{mem}$ ,计算花费的时间为$T_{math}$, 计算和访问内存可以”你算上一个，我读/写下一个“，这样两者的时间大部分都可以重叠，此时花费的所有时间就为$max (T_{mem}, T_{math})$.
$$T_{mem} = bytes/BW_{mem}$$
$$
T_{math} = ops/BW_{math}
$$
当性能受限于计算带宽时：
$$
T_{math} > T_{mem}
=>
ops/BW_{math} > bytes/BW_{mem} => ops/bytes > BW_{math}/BW_{mem}
$$
假设我们使用float16 进行计算，而A100-80G SXM 对应的$BW_{math} / BW_{mem}=312e12 flops/2039e9 bytes=153 Flops/Byte$.
即在当前显卡下，如果一个函数的计算量与所需的存储量的比值> 153 Flops/Byte 时，此时的性能主要受限于计算带宽，反之则受限于内存带宽。

如何计算一个矩阵乘法的flops
假设$A∈R^{1×n}$ ,$B∈R^{n×1}$,计算$AB$ 则需要 n 次乘法运算(operations)和n 次加法运算，对应的就是 $2n$ operations, 即$2n$ flops；同理：$A∈R^{m×n}$, $B∈R^{n×p}$ ,则需要 $2mnp$ flops.

如何计算存储大小
通常我们使用float16/bfloat16 存储，对应一个参数需要2 个bytes ,对于矩阵$A∈R^{m×n}$ 则需要 $2 \ast m \ast n$ bytes

下面做个最简单的矩阵乘法：$A∈R^{1×n}$，$B∈R^{n×p}$
$$ops/bytes = 2np / (2n + 2np + 2p) < 1 < 153$$
除了需要将矩阵读进来还需要将结果写进内存，参数使用半精度(2 bytes)，所以对应的总内存为: $2n + 2np + 2p$
此时的性能主要受限于内存带宽，如果此时将$A$ 扩大$153$ 倍至 $A∈R^{153×n}$ 消耗的计算时间是一样的，忽略内存带宽$(152 \ast 2 \ast n + 152 \ast 2 \ast p )$ bytes新增带来的影响，则扩大batch size 整体latency 基本不变。

具体深度学习Layer示例

operation	ops/bytes
Linear layer (4096 outputs, 1024 inputs, batch size 512)	315 Flops/B
Linear layer (4096 outputs, 1024 inputs, batch size 1)	1 Flops/B
Max pooling with 3x3 window and unit stride	2.25 Flops/B

GPT generation

GPT2 model architecture

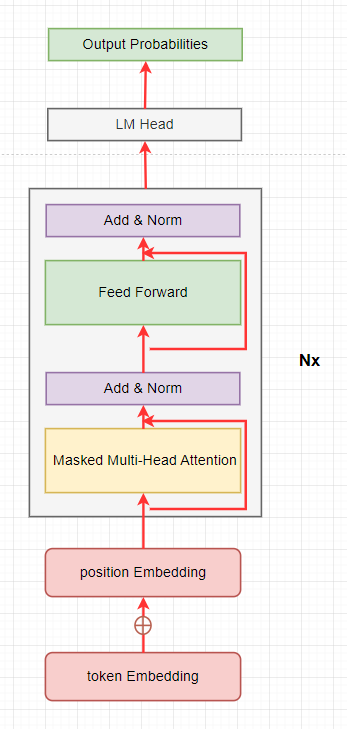
ops vs bytes

我们忽略所有的bias/layernorm/activation/add 操作,计算生成一个token 时的ops vs bytes, 切分head 与不切对应的ops/bytes 是一样的，为了简单我们按不切计算。

Embedding
multiply:$E_{token}∈R^{V\times d_{model}}$, $E_p\in R^{s_{maxseq} \times d_{models}}$
mem: $2 \ast (V \ast d_{model} + s_{maxseq} \ast d_{model})$
flops: 0
attention qkv
multiply: $t_e \in R^{1 \times d_{model}}, W_q, W_K, W_V\in R^{d_{model}\times d_{model}}, t_e \times W_q/W_k/W_v => q/k/v$
mem: $ 2 \ast 3\ast d_{model}^2$
flops: $ 2 \ast 3 \ast d_{model}^2$
attention output
multiply: $q,k,v\in R^{1\times d_{model}}, softmax((q\cdot k)\div \sqrt{d_{head}}) \cdot v => o$
mem: 0
flops: $2 \ast 2 \ast d_{model}$
output projection
multiply: $o \in R^{1\times d_{model}}$, $W_o\in R^{d_{model}\times d_{model}}$, $o \times W_o => a$
mem: $2\ast d_{model}^2$
flops: $2 \ast d_{model}^2$
feed-forward
multiply:$a\in R^{1\times d_{model}}$, $W_1\in R^{d_{model}\times 4d_{model}}$, $W_2\in R^{4d_{model}\times d_{model}}$, $a\times W_1 \times W_2 =>z$
mem: $2 \ast 2 \ast d_{model} \ast 4d_{model} = 16 d_{model}^2$
flops: $2 \ast 2 \ast d_{model} \ast 4d_{model} => 16 d_{model}^2$

剩下的计算就是重复$n\_layers$ 次2-5.现在我们来汇总一下计算总的ops / bytes:

$$
\frac{ops}{ bytes} = \frac{n_{layers} \ast (6d_{model}^2 + 4d_{model} + 2d_{model}^2 + 16d_{model}^2)} {2 \ast (V \ast d_{model} + s_{maxseq} \ast d_{model}) + n_{layers} \ast (6d_{model}^2 + 2d_{model}^2 + 16d_{model}^2)}
$$

越大的模型$d_{model}$ 越大，如10B 的模型 $d_{model}=4096$, 所以这里我们去掉$d_{model}$ 的常数项：

$$
\frac{ops} { bytes} \approx \frac{n_{layers} \ast (6d_{model}^2 + 2d_{model}^2 + 16d_{model}^2)} { n_{layers} \ast (6d_{model}^2 + 2d_{model}^2 + 16d_{model}^2)} = 1
$$

速记法
对于transformer-base encoder/decoder :
ops $\approx 2 \ast Parameters$,
float16/bfloat16 下:bytes $\approx 2 \ast Parameters$.

按照上面我们的结论，此时对于A100-80G 来说，性能主要受限于内存带宽，计算1 个token 与计算153个token 对应的latency 是一样的！为了提升整体性能，我们应该增加$batch\_size \ast input\_length$直到 inputs 扩大至153倍.

attention

现在回过头来再看一眼刚刚被我随意丢弃掉的一项ops：attention output
由于我们计算是由长度为1 的token 生成 1 个token，假设输入的token 长度为$s$, 则：
$q,k,v \in R^{s\times d_{model}}$
flops: $ 2 \ast s \ast d_{model} \ast s + 2 \ast s \ast d_{model} \approx 2 \ast s^2 \ast d_{model}$

随着inputs 的长度增加，达到$\sqrt{d_{model}}$ 时，这一项已经不能丢弃了，进一步增加，长度到$12 \ast \sqrt{d_{model}}$ 时，这一项已经与其他部分的ops 想当了，此时的$ops/bytes \approx 2$.
以10B 的模型为例，$d_{model} = 4096$ ,当输入的长度为64 时，attention output 这项ops 与其他部分想当；当长度增长为768 时，对应的$ops/bytes$ 增长到2，此时整体的计算量已经扩大了768 倍，$768 > (153 / 2 ) $，已经转变为性能受限于计算带宽，增大batch 不会带来性能提升。

cache

随着整个生成过程的迭代，输入的长度会逐步增加，对应的每步所需的计算量也指数倍的增加，整体性能都被他拖垮了。
对于$Y = A \cdot X$ ,当$X$ ,$A$ 不变时，对应的结果$Y$ 是不变的；而在迭代过程中，模型的权重是不变的，即$X$ 都是一样的，对于$step_t$ 与 $step_{t-1}$ 来说，都会计算$A[:, :t-1]$ 对应的结果，既然重叠了，就不需要重复计算了，我们每次只需要计算最后一个token 就好了。
等等，有一个层只有计算没有weights，即其对应的$A$, $X$ 都来动态的，需要我们单独处理。这一层就是attention output。（哈，又是你。attention is all I want to remove！）

对于$step_t$ 来说，对应的计算是:
$$softmax(q[:, t-1:t] \cdot k[:,0:t] \div \sqrt(d_head) ) \cdot v[:,0:t]$$
此时我们缺少的是$k[:,:t-1]/v[:,:t-1]$ ,好在我们在$step_{t-1}$ 时已经计算过这两个结果了，只要把上一个时刻的这个结果“拿到”拼接回去即可。
完整的流程是：对于迭代$step_t$ ,把对应attention qkv 的结果$q[:,t]/k[:,t]/v[:,t]$ 拼接到之前的之前的缓存$q[:,:t-1]/k[:,:t-1]/v[:,:t-1]$ 后面，为下一个时刻准备；计算attention output 时，先将之前的$k\_cache[:,t-1]/v\_cache[:,:t-1]$ 拼接到$k[:,t]/v[:,t]$ 前面，还原真实的$k/v$.

经过cache 后，attention output 的计算回到了$O(s\cdot d_{model})$ 的水平，至少在大部分时候又可以基本忽略了。此外，随着$s$ 的增长，对应的cache 也在线性增长，需要的内存带宽也在增长，所以有些情况下可能增加cache 反而降低性能。

PS:不管是生成过程中的k_cache/v_cache 还是prompt cache 还是context cache，只要是可能重复计算，就值得思考要不要将之前的结果做cache，已减少后续的计算量。

定量评估优化方案

上面是一个相对简化的思路计算，而真实情况会比较复杂。比如我们忽略了一部分操作所需的ops；中间结果的每次写入/读取所需的内存带宽；CUDA Core 与 Tensor Core 的性能差异等；此外不同的硬件参数也不相同，具体的operation 实现也不相同，所以要定量给出优化方案实在太难，通常（主要是我）只能通过测试给出大致范围。