最近有篇很火的论文bert-flow，其中的flow是出了GAN和VAE之外的第三种生成模型，我竟然是第一次听说，所以引起了我的好奇心，然而看flow模型时，发现里面有一个很重要的概念就是行列式，数学渣太久没碰过他所以再看到有些陌生，于是就找了一些文章来重新学习一下，后来发现了孟岩的认识矩阵系列博客与苏神的新认识矩阵系列博客，看完感觉对矩阵的认识refresh了一下，所以做一些总结记录。

什么是1

首先我们来讨论一下，什么是1，所谓1，就是参照物，或者是基，而其他的数字都是在参考他得到的，比如2,2就是2 个1，也就是12.
而1又是一个抽象的东西，你没法直观感受什么是1，只有在参考系下，才能直观感受到什么是1，如1瓶水，1米长，而1 与一米的关系就像类与对象一样。所以在参考系下，2米的含义就是2个1米，1米 2，即在以1米为基的坐标系下，他在2的“位置”。而5瓶水，对应的含义是在以1瓶水为基的参考系下，
他处在5的“位置”。而不同的坐标系，在不同的情况下也有优劣之分，如同样的酒，当用来统计销售额时，我们用“瓶”来统计就比用“杯”来统计方便，而当用来劝酒时，用“杯”就明显比用“瓶”要合适一些。也就是，酒还是那么多酒，但是当你用不同的方式来度量时，得到的结果也是不同的，是有优劣之分的。

向量

对于向量$A(a, b)$,其对应的含义是在直角坐标系（以$\vec{i}=(1,0),\vec{j}=(0,1)$为基）中，A是在x轴上为a,y轴上为b的点。
比如，在以x轴为斤y轴为瓶的直角坐标系（以$\vec{i}=(一斤,0瓶), \vec{j}=(0斤,1瓶)$为基）中，三瓶500毫升的肥仔水对应的向量就是B(3,3).所以，所谓向量即在线性空间内，选定一组基后，用来刻画一个对象。

矩阵

那何为矩阵呢？比如对于矩阵
$$A=\begin{pmatrix}
a & c \\
b & d
\end{pmatrix}$$
我们能观察到什么呢？首先，矩阵也是由向量（列向量）组成的，对于当前矩阵A，也就对应着$\vec{i}=(a,b),\vec{j}=(c,d)$ 两个向量，然后将他们按一定的顺序排列就组成了矩阵；此外，这个矩阵又代表了由这两个向量为基组成的坐标系（线性空间），在这个空间内，所有的对象都能通过这两个基来进行刻画，即对应于一个“向量”。这里如何更直观的理解呢？还是考虑之前的例子，同样是酒，我们可以用“杯”来度量，也可以用“瓶”来度量，假如我们用“杯”作为最初的基，
那矩阵对应的就是“瓶”作为基构成的坐标系，而构成矩阵的向量又是在以“杯”为基下度量出来的，其对应的向量中的值的含义就是“瓶”的基在“杯”这个基下的表示，
同样的酒，假如在“杯”坐标系下为10（杯），通过这个矩阵，就变为了2（瓶），即矩阵是线性空间里变换（运动）的描述。

矩阵乘法

那何为矩阵乘法呢？比如现在有矩阵
$$
A=\begin{pmatrix}
a & c \\
b & d
\end{pmatrix}
$$
向量$x=(e,f)$,对于$Ax$这个矩阵与向量的乘法，这个是什么含义呢？上面我们已经提到了，矩阵是由列向量组成的，而列向量又可以看做是对应坐标系下的一组基，那根据之前我们提到向量与基的关系，就是在基确定后，用来刻画其空间内对象的，对应的就是乘法，那这个矩阵与向量的乘法，我们也可以用这种方式来看待，即矩阵与向量的乘法代表的是在矩阵对应的列向量为基组成的空间内，由向量刻画的对象。这也是为什么矩阵乘法要求对应维度要相等，
对应的就是需要用所有的基，才能正确刻画在这组基对应坐标系下的位置（对象）。而矩阵与向量乘法就是用新的基来刻画对象，也即矩阵与向量的乘法代表施加变换。

那为什么矩阵的乘法公式里为对应行与列相乘并求和呢？这是因为最终的结果，我们是需要变换到对应的直角坐标系下的，因为我们书写出来的所有向量，都默认是在直角坐标系下的结果，所以我们需要将结果向量在每个轴上进行分解，然后合并得到最终的结果，对应的就是行与列相乘后求和。

那何为矩阵与矩阵的乘法呢？如$A * B$,同理，矩阵与矩阵的乘法也可以看做是连续变换后，构造的新的坐标系。矩阵是由向量组成的，而矩阵与向量乘法的含义是在新的基下刻画的对象表示，所以矩阵与矩阵的乘法，对应B这个变换在施加了A这个变换后，形成的新的变换，而施加这个变换，对应B中的列向量都是在A坐标下刻画得到的。

那何为线性方程呢？比如$Ax = y$, 对应的线性方程是什么含义呢？这个方程左侧有向量有矩阵，而右侧缺只有向量，有点不和谐，我们变换一下，让他们形式一样，$Ax = Iy$,这样，等式成立，两边形式也一样。那写成这个变换，我们就能猜到这个方程中等式的意义了：在直角坐标系($I$)下的y向量，在A坐标系下该如何刻画(x)呢？那再来看看这个方程的解，即$x = A^{-1}y$，而这个式子可以理解为将施加的变换“逆”着再变回去，就还原了原始位置。

普通乘法有交换律、结合律、分配律，那矩阵乘法是否也满足呢？对于交换律，矩阵乘法是不满足的，想象一下，5“瓶”酒换成“杯”可能是25，而5“杯”酒换成“瓶”，可能也就是1了，所以两个变换交换位置，得到的是不同的变换；而结合律与分配律是满足的，结合律可以看做是将变换分成“几步”走，即先进行“子变换a”,在进行“子变换b”，几步走与一步到位的结果是一致的；而分配律也是类似的思路。

相似矩阵

那何为相似矩阵呢？假设有一个矩阵A，对应$y=Ax$, 而现在有一个新的坐标系P，对应有${y}’=B{x}’$,在P坐标系下，x与y对应着$P{x}’=x$, $P{y}’=y$,代入后得到：$P{x}’=AP{y}’ = P(P^{-1}AP){x}’$，即在P坐标系下，从${x}’$ 到${y}’$的变换用矩阵$B=P^{-1}AP$来表示，这就是相似矩阵，即同一个线性变换在不同坐标系下的一个测量结果而已。

行列式

行列式是在通过高斯消元法解线性方程组时引入的数学工具, 对应的定义为：
$$
D = \sum(-1)^t a_{1p_n}a_{2p_n}…a_{np_n}
$$
其中$t$为排列$a_{1p_n}a_{2p_n}…a_{np_n}$的逆序数，$\sum$ 为对所有可能的排列求和。
这个计算方式看起来好奇怪，还有一个逆序数，无法直观的理解，那怎么才能有个直观印象，让我们知道为什么这里是这么计算的呢？
说实话我虽然几年前在网易云课堂重新学了一遍线性代数，但是今天又基本全忘记了，所以这次，我希望找到一些更“直观”的东西。
如果按照矩阵就是对应坐标系的变换，也就是对应基的变换的思路，那矩阵的行列式应该是对应着变换的某种度量（实际是对应坐标系的缩放，也就是基的体积变换）。顺着这个思路，苏神的一篇博文新理解矩阵5：体积=行列式中，通过两者的性质相同，证明了行列式的几何意义，就是其对应的n维平行n维体的体积。
知道了这个，我们就可以尝试通过计算平行n维体的体积来“直观”感受一下了。

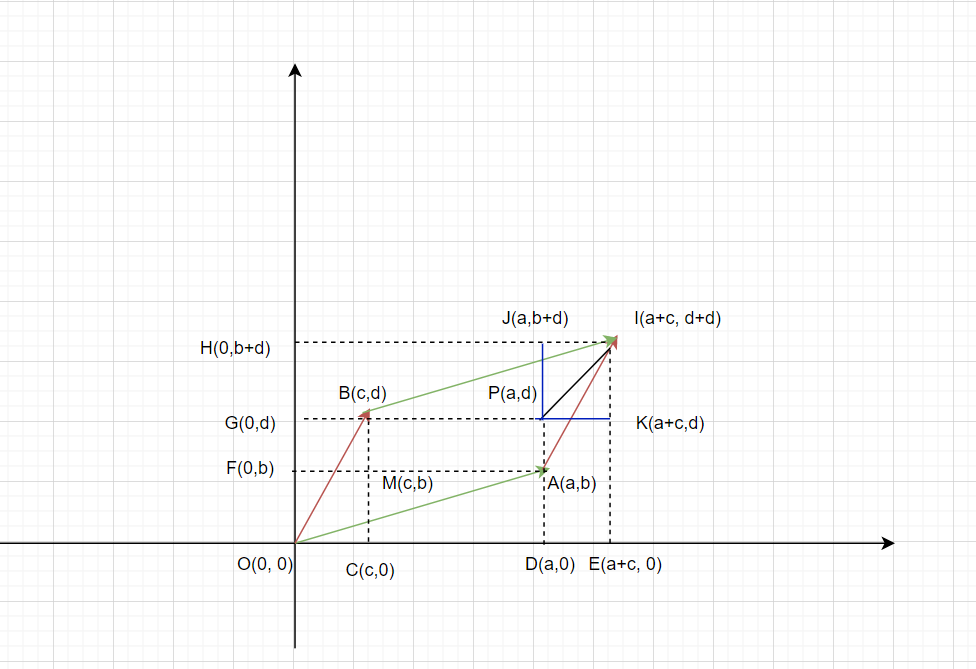
这里我们讨论二维空间，如上图所示，其中$\overrightarrow{A}$与$\overrightarrow{B}$分别代表两个向量，而其围成的面积S 为(O,A,I,B)四个点所围成的图形。而这个图形又可以看成两个部分的组合：一部分为与四边形(O,D，P,G)重叠的部分，另一部分为剩下的部分。而剩下的部分又可以通过$PI$切分为两个三角形：$\bigtriangleup BPI$ $\bigtriangleup API$，
我们分别做两个三角形的高（蓝色线）$PJ=b, PK=c$，此时我们将$\bigtriangleup BPI$ 与 $\bigtriangleup ODA$ 进行对比，两者的高都是$b$,而底的差为$c$，也就是$S\bigtriangleup ODA - S\bigtriangleup BPI = S\bigtriangleup OCM$， 类似的，我们可以求出$S\bigtriangleup OBG - S\bigtriangleup API = S\bigtriangleup OFM$,于是，我们就可以得到一个结论：
$$
S_{\square OAIB} = S_{\square ODPG} - S_{\square OCMF} = ad - bc = \begin{Vmatrix}
a &b \\
c & d
\end{Vmatrix} = det(A,B)
$$

而两个四边形的位置都是由向量在坐标轴上投影后确定的，也就是对应着行列式中的“排列相乘”，而面积不足需要被“减掉”的小面积就对应逆序数，所以完整的过程就是“通过排列求长方形的面积，然后用大面积减去小面积”。
以上的思路可以推广到N维空间，思想是一样的。 而理解了矩阵的行列式就是平行N维体的体积后，对应行列式的计算公式也就显得相当“直观”了。如，对行列式的某一列乘上$\alpha$，则对应的行列式的值也乘上$\alpha$，这里就是对应其中的一个基向量放大了$\alpha$倍，所以体积放大了$\alpha$倍。

总结

本文主要是参考了许多文章后，发现将矩阵看做是变换的表述这个视角下，很多相关问题都变得非常直观又容易理解，最后经过思考做的部分总结，如果对矩阵感兴趣或者总觉得不容易理解，推荐孟岩的理解矩阵系列、苏神的新理解矩阵系列、马同学的矩阵与行列式系列

关于头图

Buy me a coffee

如果觉得这篇文章不错，对你有帮助，欢迎打赏一杯蜜雪冰城。