对Adam 进行改进的算法有很多，今天介绍一篇改动很小改动小效果不错的-AdaBelief。

warmup

在bert中第一次见到warmup的使用，而warmup的作用是让训练更稳定，最后收敛的更好。而warmup有效的一个原因是减缓训练初期模型对mini-batch的提前过拟合，同时，在训练初期，由于loss较大，模型还没得到多少训练，不同step 之间的梯度方差较大，而此时如果使用较大的步长更新，则会朝错误的方向走一大步，而随后的模型不断得到训练，对应的梯度不断减小，同时一般我们会采用不断衰减的学习率，这些都导致随着模型的训练，更新的步长不断变小，而前期朝错误方向的一大步更新可能需要后期很多步的更新才能弥补，有时候可能甚至无法弥补，这就导致模型最后收敛在一个不怎么好的局部最优点，而如果在前期时抑制可能出现的大步更新，保持模型保持“小步走”，则可以避免模型在错误方向上的大步更新，而由模型的不断训练调整会正确的轨道。
所以一个重要的点是梯度更新方差大时（不同time step），我们需要谨慎行事，防止出现大错步，而方差小时，我们可以大胆一些，因为此时方向上基本一致，所以可以大踏步的往前走。

修改Adam

现在让我们来回顾一下Adam更新公式：

$$
\theta_t = \theta_{t-1} - \alpha \frac{m_t}{\sqrt{v_t}}
$$

其中$m_t$是对$g_t$的预测，$v_t$是对$g_t^2$的预测，对应的更新方向为$\frac{m_t}{\sqrt{v_t}}$.
$m_t$除了是对$g_t$的预测外，还可以看做是最近一段时间内（大概为$\frac{1}{1-\alpha}$）梯度的均值,而为了表征当前梯度$g_t$所处区域的方差，我们可以使用$belief = \left | g_t - m_t\right |$,即当前梯度距最近一段区域梯度均值的距离。在结合Adam的更新公式，我们可以用$s_t = (g_t - m_t) ^ 2$ 来代替$v_t$,即在方差大的区域更新时减小步长，而在方差小的区域，快步大走，最后的更新公式为：

$$
\theta_t = \theta_{t-1} - \alpha \frac{m_t}{\sqrt{s_t}}
$$

此时的更新方向为$\frac{m_t}{\sqrt{s_t}}$.
这就是AdaBelief Optimizer的核心思想。具体的更新流程与Adam只需要修改一小部分即可：

优点

作者在论文中提到AdaBelief能媲美Adam的收敛速度，同时达到SGD的准确率。我做了几个实验，由于是在小数据集上fine-tuning，所以可能不如在大数据集上从头训练效果明显。不过依然可以得到：
1.loss上相对Adam更平稳
2.收敛上比Adam稍快
3.性能上比Adam更好

loss 对比图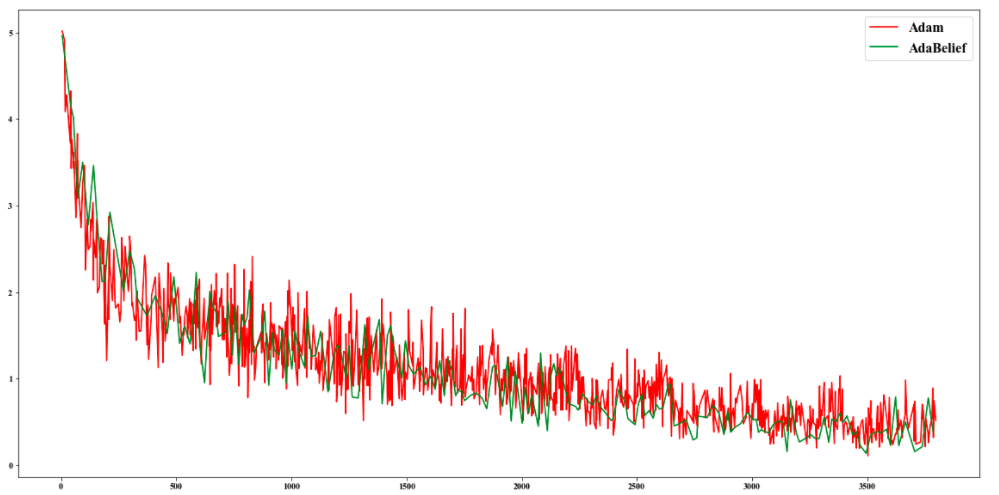

accuracy对比图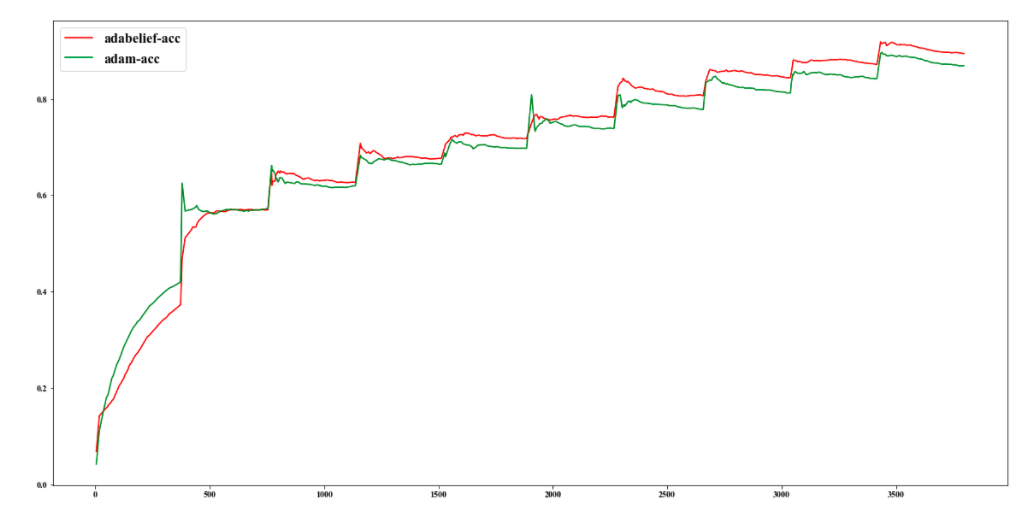

实验代码：classification_adabelief

总结

本文介绍一个最新的优化器AdaBelief，并从与论文不同角度解释其主要作用，在实际工作中可以尝试使用AdaBelief，也许能得到比Adam收敛更快性能更好的结果。

关于头图

算法改进对比图