听到一个题目，还挺有意思，所以记录一下。

题目

问：一个绳子长a，任意剪两刀变成三段后，可以组成一个三角形的概率是多少？

解答

分析一下题目，一段长度固定的绳子，切割为三段，则：
1. 任意一段绳子的长度大于0小于a；
2. 任意两段绳子的长度大于0小于a。

而三段绳子可以组成一个三角形，而三角形中两边之和大于第三边，所以意味着：
1.任意一段的长度小于a/2；
2.任意两段的长度和大于a/2.

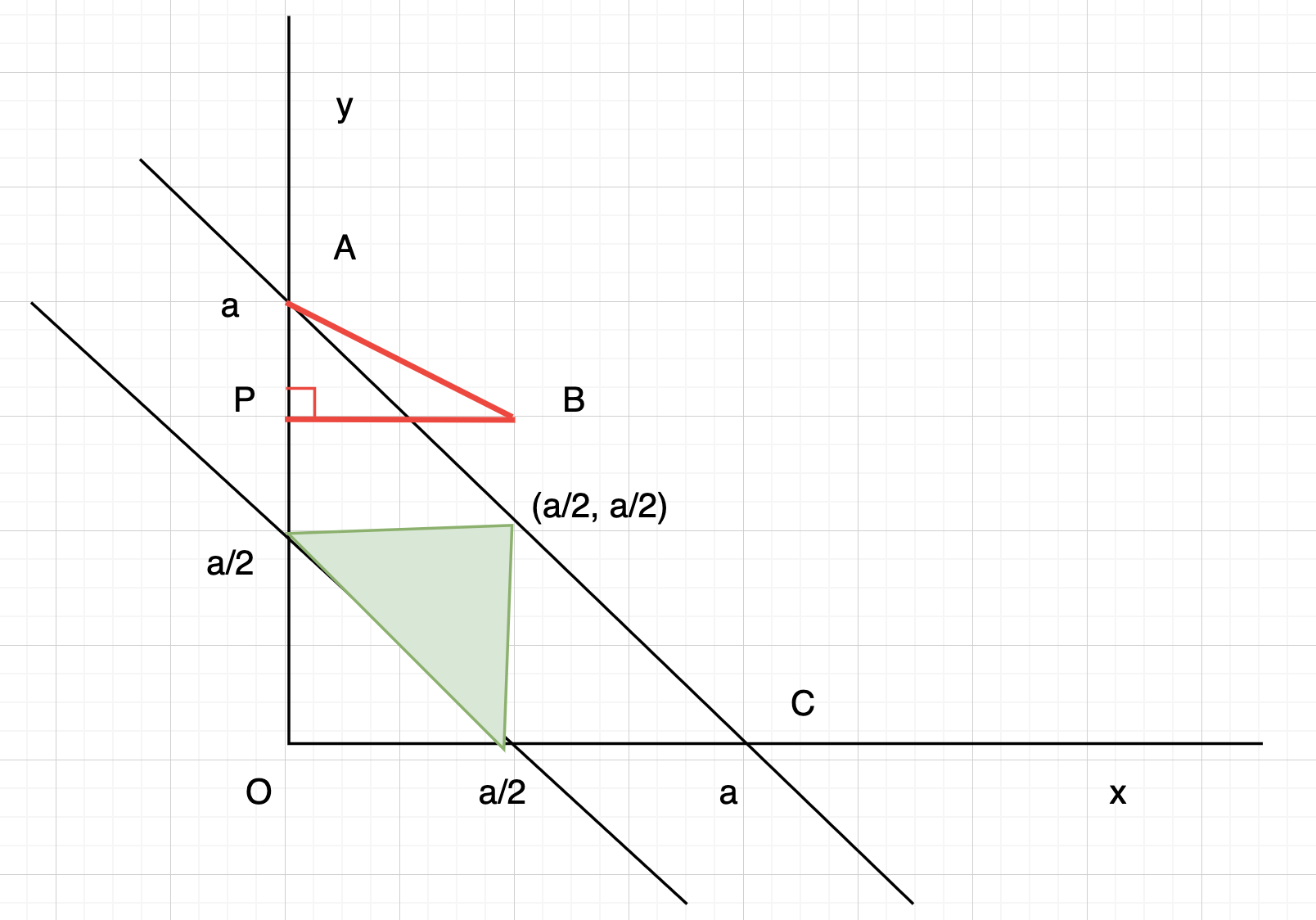
现在设其中两段的长度分别为 x, y，画出一个直角坐标系，如下图所示。

同时连接(0, a), (a, 0)两点，则切割绳子后其中两段的长度的所有可取的值对应由(0, 0),(a, 0), (0, a)组成的三角形区域。
简单证明如下：对于任意一点B,我们做其对y轴的垂线，相交与点P,而点B位于(a, 0) (0, a)的连线时，对应$\angle PAB = 45^o$,此时
$PB=PA \Rightarrow PB + PO = PA + PO = a$,而当P位于连线外侧，则$\angle PAB > 45^o$,对应$PO + PB > PO + PA = a$,不满足约束。而$\Delta A O C$ 的面积为 $a^2 / 2$.

而对于能组成三角形时，首先任意一条长度小于$a/2$，对应(0, a/2),(a/2,a/2)连线与(a/2,0)(a/2,a/2)连线围城的矩形区域，而任意两边之和大于$a/2$,利用之前的方法可以证明是(0,a/2)(a/2, 0)连线右侧区域，两者的交即图中绿色三角形区域，其面积为$(a/2)^2/2 = a^2 / 8$

所以最后结论是组成三角形的概率为两个面积之比：
$$
pro = \frac{a^2/8}{a^2/2} = 1/4
$$

关于头图

Buy me a coffee

如果觉得这篇文章不错，对你有帮助，欢迎打赏一杯蜜雪冰城。