样本不均衡之难易不均衡

小蛋子

2020-10-14

Cross Entropy
样本类别不均衡
Focal Loss
- 如何确定$\alpha$ 与 $\gamma$
- 实验
GHM
总结
关于头图

上篇看样本下菜的FastBERT提到样本有难易，通过利用样本的这个特性，可以在推理上进行加速，除了在推理上可以利用，在训练时也可以利用，本篇就来说怎么在训练时更充分的利用样本有难易的特性。

Cross Entropy

对于分类问题，通常我们选择交叉熵作为损失。本文均针对二分类进行说明，多分类的情况可以横向扩展。对于二分类问题来说，其损失CE：

$$
CE = \left\{\begin{matrix}
-log(p)& y\_true=1 \\
-log(1-p),& y\_true=0
\end{matrix}\right.
$$

样本类别不均衡

当我们遇到一个正负样本不均衡的情况，如1:1000时，直接训练后效果往往不好，其倾向于将更多的样本预测为类别多的类，而产生的原因是：由于我们训练时使用的 CE:
$CE_W = CE_positive + CE_negative$, 其中CE_positive 与 CE_negative 分别代表正负样本的loss，而由于此时的样本不均衡，loss主要有类别多的样本贡献，主导了优化方向，所以模型会偏向数量多的方向，如当前全部预测为正样本，那解决这个问题最简单直接的办法就是在loss上增加一个权重α来均衡一下两方的loss，从而让模型更“公平”的对待不同类别样本,即：

$$
CE_W = \left\{\begin{matrix}
-\alpha log(p)& y\_true=1 \\
-(1-\alpha)log(1-p),& y\_true=0
\end{matrix}\right.
$$

Focal Loss

除了在类别上可能存在这种不均衡外，样本在难易程度上往往也会有难易之分。如当训练一个情感分类器时，“不喜欢xx”就比“谁不喜欢xx呢”要容易训练一些. 为了衡量这种“难易”特征，我们定义一个代表预测值与真实label 之间差距的参数$p_t$:

$$
p_t = \left\{\begin{matrix}
1-p,& y\_true=1 \\
p,& y\_true=0
\end{matrix}\right.
$$

即

$$
p_t = \begin{vmatrix}
pred - y_{true}
\end{vmatrix}
$$

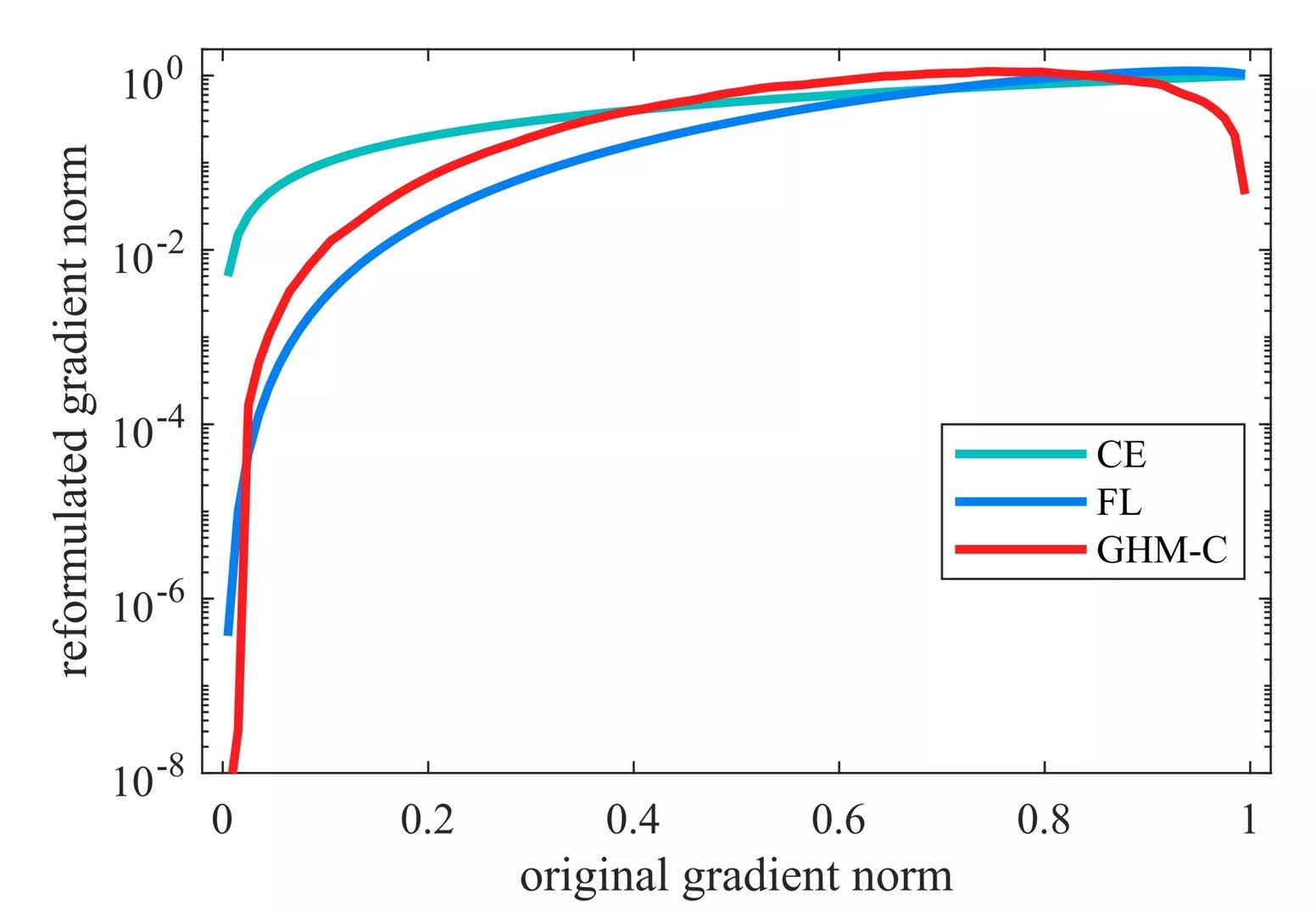
pt越大则说明预测值与其label 相差越大，也即样本越“难训练”，最后我们对整个样本的pt 统计往往得到一个U型分布，如下图所示：

即“易训练”样本是“难训练”样本的指数级。虽然此时“易训练”样本由于得到了很好的训练，其loss 很小，当由于其数量庞大，任然可能主动整个训练。
所以为了解决难易不均衡的问题，我们采用与样本不均衡一样的方法：对不同样本添加一个权重来平衡，即此时的loss FL:

$$
FL = \left\{\begin{matrix}
-\alpha \beta(p\_t) log(p)& y\_true=1 \\
-(1-\alpha)\beta(1-p\_t)log(1-p),& y\_true=0
\end{matrix}\right.
$$

而前面我们说难易样本的loss 呈指数级差距，所以此时的$\beta(p_t)$ 我们也定义为指数函数，最终的 FL:

$$
FL = \left\{\begin{matrix}
-\alpha(1 - p)^{\gamma} log(p)& y\_true=1 \\
-(1-\alpha)(p)^{\gamma}log(1-p),& y\_true=0
\end{matrix}\right.
$$

此时，$\alpha$ 用来平衡样本不均衡，$(1-p)^{\gamma}$ 用来均衡难易样本。通过平衡难易样本对应损失，让模型更“关注”那些难分的样本。

以上就是focal loss 的主要思想，虽然最后我们得到的loss形式上与focal loss一样，但其中参数的含义与focal loss中的内容却有一些不同，主要在于focal loss 中实验证明，由于对难易样本降权后正样本（量少的类）对应的loss反而更易主动优化方向，所以用 $\alpha$ 来降权，而我们上面提到的alpha 主要是用来均衡正负样本，这里读者可以自行判断理解。此外，苏剑林通过硬截断过渡到软阶段也得到了类似的loss，推荐大家也看看：从loss的硬截断、软化到focal loss

如何确定$\alpha$ 与 $\gamma$

在focal loss论文内，作者是通过搜索一个范围来确定两个参数的最优解，最后给出的结果是 $\alpha = 0.25$, $\gamma=2.$，而通过上面我们提到的两个参数的含义，这里给出一个确定参数范围的方案：
1.首先，我们通过统计正负样本，来确定$\alpha$的大致范围；
2.通过CE_W我们可以训练一个基础的分类器，通过这个分类器，我们对训练集进行预测，生成对应的prob，然后通过统计$p_t$，我们认为$p_t<=0.1$ 的为主要的“易分样本”，${p_t>=0.9}$ 为主要“难分样本”，由于是指数衰减，所以两者的loss 差距为 $9^\gamma$, 即此时$9^\gamma=C_易/C_难$, 解出此时的$\gamma$ 即可得到其大致的范围。

实验

实验时，通过构造一个正负样本8:1的数据集进行实验，在通过权重平衡正负样本不均衡后，对应的pt分布如下图：

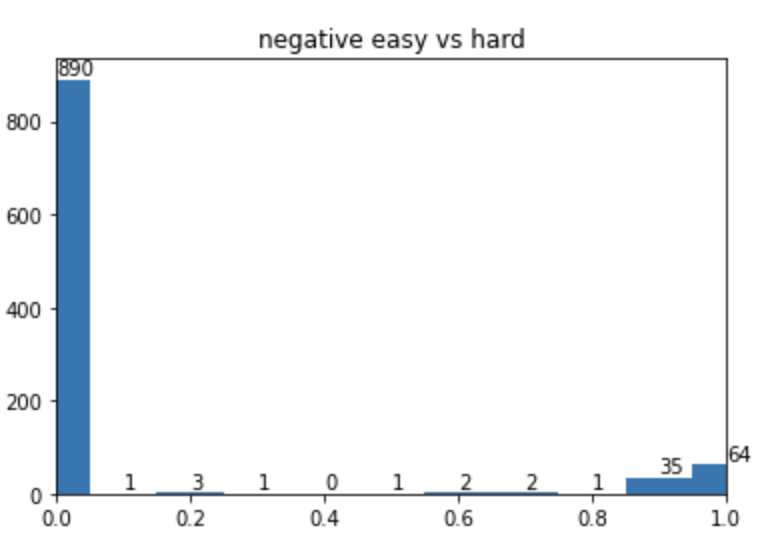
而focal loss 训练后的pt 分布为：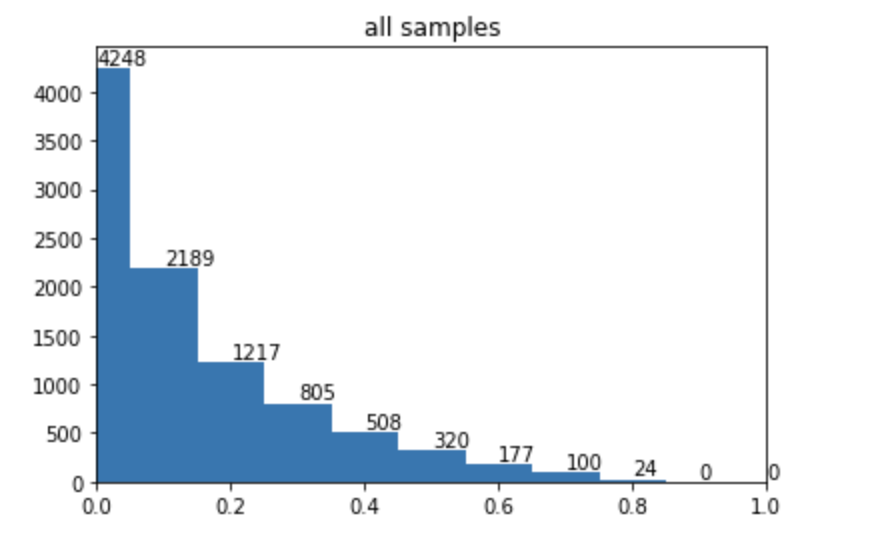

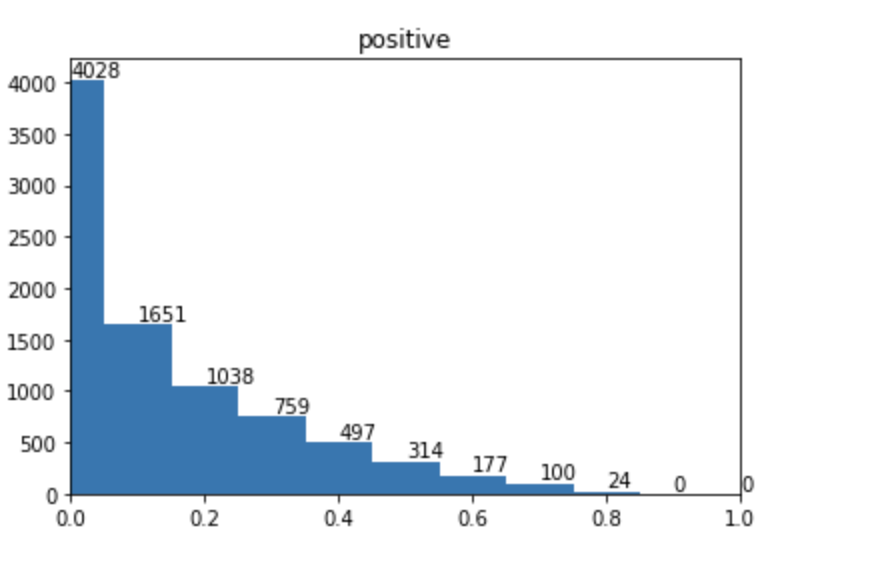
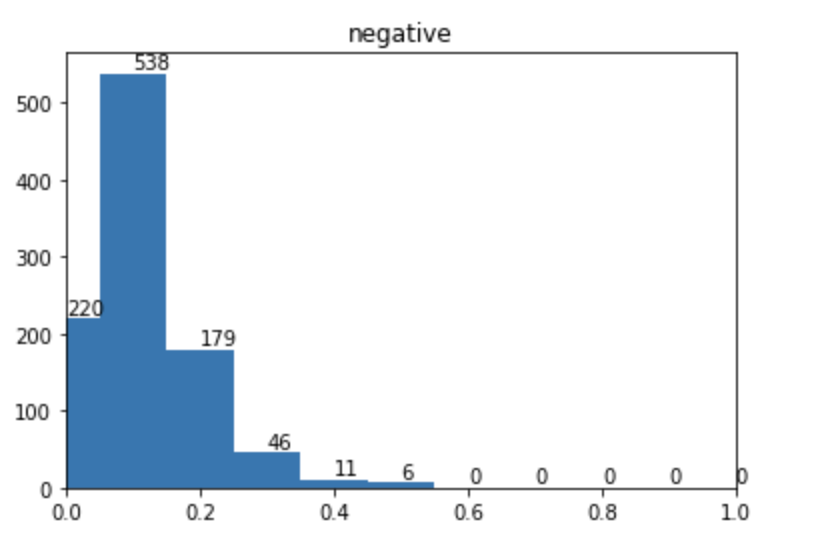
可以看到，在focal loss 下，右侧偏差大的样本基本都被移到了左侧，说明“难样本”大幅度减少变为了“易样本”。
实验代码地址：classification use focal loss

GHM

现在让我们来讨论一下focal loss存在的问题：

首先，让模型过多的关注那些特别难分的样本没有什么问题，但是这个前提：样本紧凑。而当数据中存在离群点时，那此时就会发生：本来模型已经收敛了，但是由于这些离群点还是会误判，一直存在在pt的最右侧，而让模型再过多的去关注这些点，这明显是不合适的；
对于focal loss中的两个参数$\alpha$ 和$\gamma$ ，虽然我们能估算一个大致范围，但是由于两者是相互影响的，所以实际使用时还是需要通过实验去寻找最优解，这也为训练增加了一定的难度。

现在再让我们回过头来重新审视一下我们的原始问题：样本有难易之分，所以训练时存在难易样本不均衡，而”易分”样本占比过高导致主导优化方向。那此时让我们往后再思考一步，当我们对易分样本降权后，对应的pt分布图中最左侧的柱子会降低，而由于模型得到了更好的优化方向，模型的性能提高，所以最右侧的柱子也会降低，两边减少的样本会同时向”中间”扩散，最后得到一个比原始pt分布曲线更”平滑”的分布曲线，正如上文中focal loss对应的pt分布图。
而focal loss 由于过度关注”难分样本”，导致存在离群点时不理想的问题。而离群点有一个特点就是：量相对正常样本非常少（否则就是一个”小群”了），利用这个特点，我们就能对focal loss 进行改进了。改进的思路就是利用离群点少的特点，从难易样本的量上来平衡难易样本的loss。
具体做法：我们将$p_t$ 按间隔$\varepsilon$均等的分为K个区间，然后统计不同区间内的样本数量$num_k$，然后针对每个区间内的loss 我们用参数$\beta(i)$ 来平滑：

$$
L_{GHN-C} = \sum_{1}^{N}\beta(i)L_{CE}(p_i, \hat p_i)
$$

其中：
$\beta(i)$对应$pt_i$所属区间的样本$num_k$在整体样本 $N$ 中占比的倒数。
而在实现时，由于通常我们都是采取mini-batch 的方式训练，无法在每个batch内事先得到全局统计量进行$\beta(i)的计算，一种近似的办法是利用动量，逐步近似求。
以上就是GHM 在分类情况下的loss，原始论文中的pt 分布对比图中也能看到，利用GHM确实更平滑。