
Knowledge Distillation (1) : 模块替换之bert-of-theseus-上篇
如果忒修斯的船上的木头被逐渐替换,直到所有的木头都不是原来的木头,那这艘船还是原来的那艘船吗?-普鲁塔克
最近遇到一个需要对算法加速的场景,了解到了一个比较简洁实用的方法:Bert-of-theseus,了解了原理后参考代码实验后,验证了其有效性,所以总结一下。
模型压缩
模型在设计之初都是过参数化的,这是因为模型的参数量与复杂度代表着模型的容量与学习能力,但当我们实际使用时,我们需要更好的部署他(低资源),更快的响应(快速推理),常常需要进行模型压缩。
模型压缩就是简化大的模型,得到推理快资源占用低的小模型,而想”即要马而跑又不用吃草”通常是很难的,所以压缩后的模型常常也会有不同程度的牺牲,如模型性能下降。
此外,模型压缩是作用在推理阶段,带来的常常是训练时间的增加。
模型压缩又分为三种方式:一种是剪枝(Pruning)与量化(Quantization),一种是知识蒸馏(Knowledge Distillation),还有一种是权重共享(Sharing)与因数分解(Factorization)。该部分内容推荐一篇博客:All The Ways You Can Compress BERT
剪枝
剪枝技术是通过将大模型中一些”不重要”的连接剪断,得到一个”稀疏”结构的模型。剪枝又分为”结构性剪枝”与”非结构性剪枝”.剪枝可以作用在权重粒度,也可以作用在attention heads / layer粒度上。不过剪枝技术感觉会逐步被
量化
量化不改变模型的网络结构,而是改变模型的参数的数据格式,通常模型在建立与训练时使用的是 float32 格式的,量化就是将格式转换为 low-bit, 如 float16 甚至二值化,如此即提速又省显存。
知识蒸馏
知识蒸馏是训练一个小模型(student)来学习大模型(teacher),由于大模型是之前已经fine-tuning的,所以此时学习的目标已经转换为对应的logit而
不再是one-hot编码了,所以student有可能比teacher的性能更好。这样即小又准的模型实在太好了。不过为了达到这样的效果,通常设计小模型时不
光要学习大模型的输出,还要学习各个中间层结果,相关矩阵等,这就需要仔细设计模型的结构与loss及loss融合方案了。一种简单的方法是只学习大模型的logit,这与对label做embedding有点类似,不过我没做过实验还。
权重共享
将部分权重在多个层中共享以达到压缩模型的效果,如ALBERT中共享self-attention中的参数。
权重分解
将权重矩阵进行因数分解,形成两个低秩的矩阵相乘的形式,从而降低计算量,如ALBERT中通过将Embedding分解降低参数量。
模型压缩的必要性
看了上面模型压缩的方法,每一个都有种”脱裤子放屁”的感觉,与其训练一个大模型,再费力把它变小,为何不直接开始就弄个小的呢?
首先,模型在设计之初是都是会或多或少的过参数化,因为模型的参数量与复杂度代表着模型的容量与学习能力;
其次,开始就用一个小模型,那这个小模型也是需要设计的,不能随便拿来一个,而设计一个性能高参数规模小的小模型难度是非常大的,往往是模型小了性能也低了;
第三点,大模型压缩后与小模型虽然参数规模相当,但是对应的模型空间并不相同。
此外,为了更好的部署,如手机或FPGA等,得到精度更高模型更小(distillation)或者利用硬件加速(low-bit),模型压缩都是值得试一试的手段。
更详细的讨论,可以参考为什么要压缩模型,而不直接训练一个小的CNN
Bert of theseus
Bert of theseus 方法属于上面提到的知识蒸馏,知识蒸馏中我们提到,在蒸馏时,我们不光要学习teacher的输出,对中间层我们也希望他们直接尽量相似,
那想象一个这种状态对应对理想情况:中间层的结果一致,最终的结果一致,既然我们的期望中间结果一致,那也就意味着两者可以互相替换。
正如开头提到的忒修斯之船一样。所以核心思想是:与其设计复杂的loss来让中间层结果相似不如直接用小模型替换大模型来训练
通过复杂loss来达到与中间层结果相似可以看作是一种整体渐进式的逼近,让小模型一点点去学习,而直接替换可以看作是一种简单粗暴的方式,
但是他不需要设计各种loss,优化目标也是同一个,就只有一个下游任务相关的loss,突出一个简洁。
这就好比高中上学一样,即使花高价也要让孩子去一所好高中,因为学校的”氛围”能让孩子的学习成绩进步,其实是因为周围的孩子带着一起学,
弱鸡也能学的比平时更多一点。bert-of-theseus也是类似的道理,跟着大佬(teacher)总比单独fine-tuning效果好。
具体流程
如果直接将小模型替换大模型,那其实是在对小模型进行微调,与大模型就脱离了,也达不到对应的效果,所以作者采用了一种概率替换的方式。
首先呢,想象我们现在已经训练好了一个6层的BERT,我们成为Predecessor(前辈), 而我们需要训练一个三层的bert,
他的结果近似12层BERT的效果,我们成为Successor(传承者),那 bert-of-theseus的模型结构如下图所示:
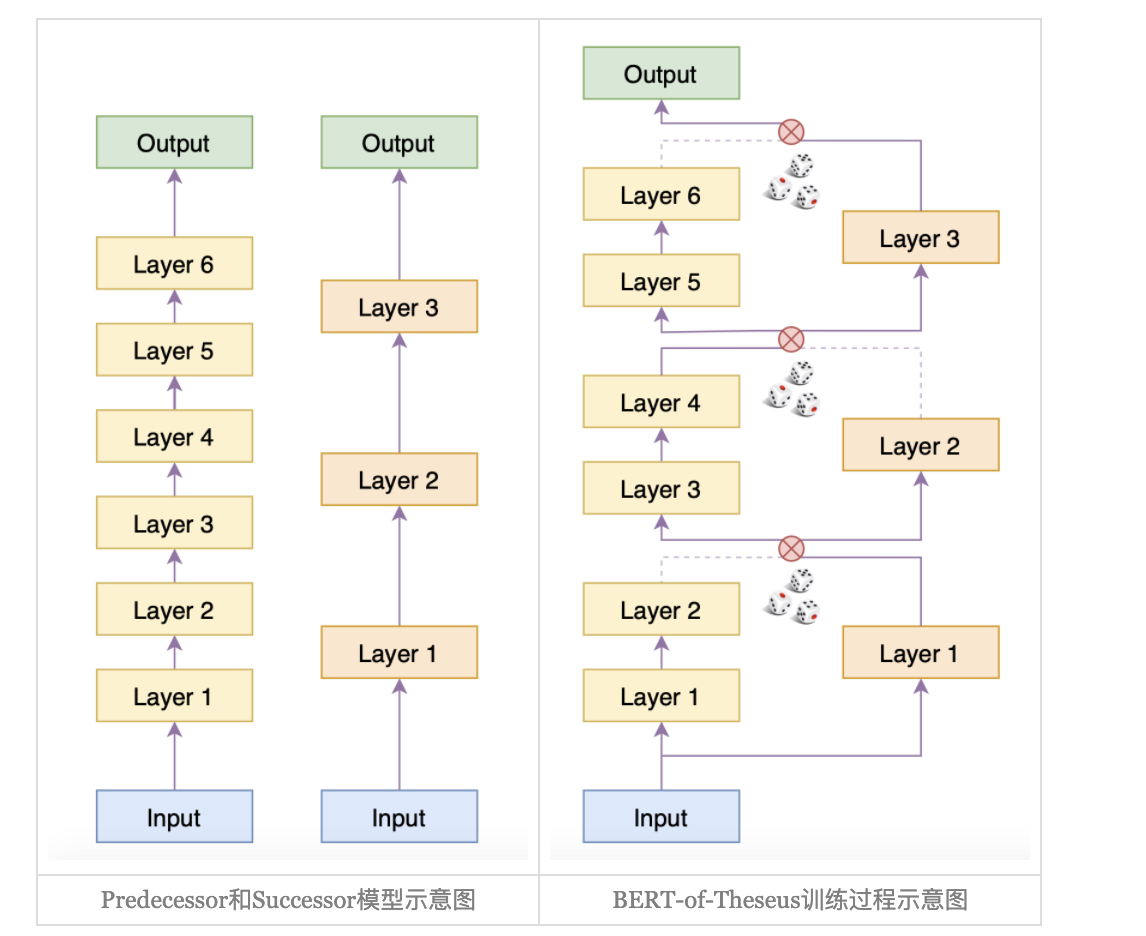
在bert-of-theseus中,首先固定predecessor的权重,然后将6层的Bert分为3个block,每个block与successor的一层对应,训练过程分为两个stage:
首先用successor中的层概率替换predecessor中对应的block,在下游任务中直接fine-tuning(只训练successor),
然后将successor从bert-of-theseus中分离出来,单独在下游任务中进行fine-tuning,直到指标不再上升。
所谓替换,就是输出的替换,在进入下一层前在predecessor和successor的输出中二选一。
替换概率作者也给出了两种方式,一种是固定 0.5,一种是线性从0-1,如下图所示: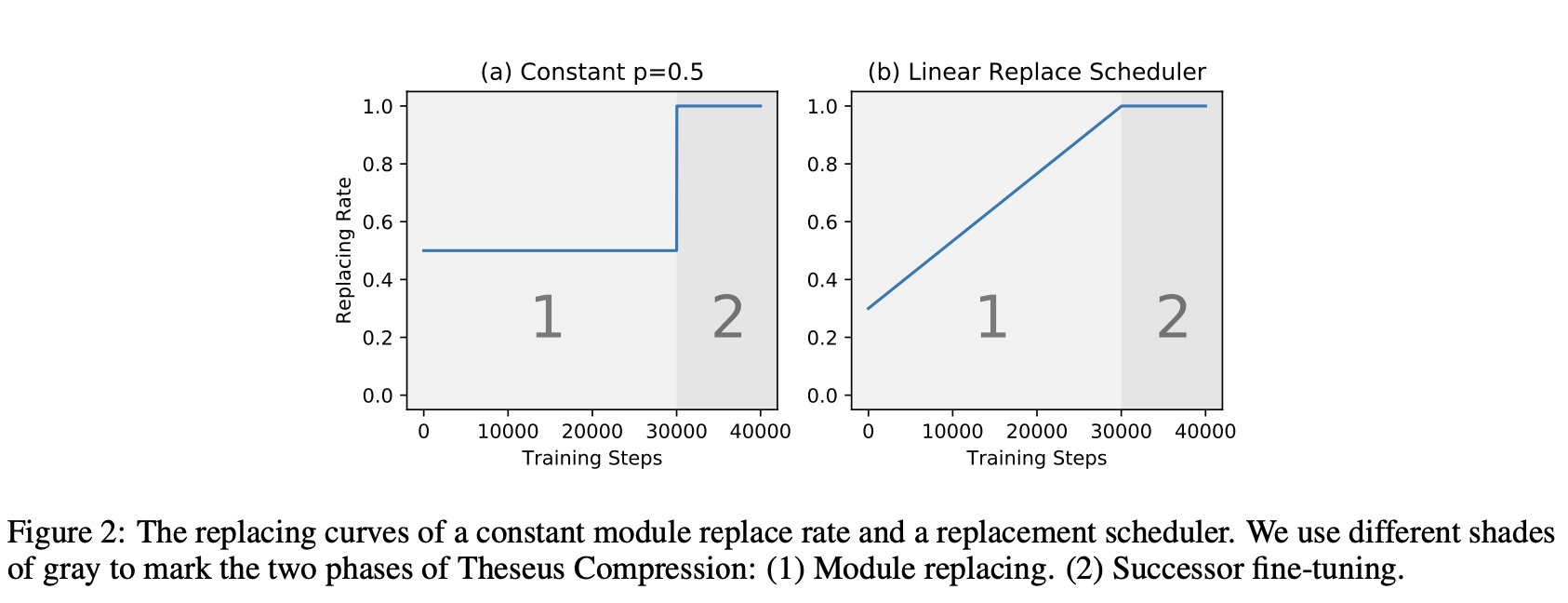
实验效果
实验代码主要参考bert-of-theseus, 实验主要做了三组,一组文本分类两组ner-crf,结果如下:
文本分类:CLUE的iflytek数据集
| 直接微调 | BERT-of-Theseus | |
|---|---|---|
| 层数 | 完整12层 / 前6层 / 前3层 | 6层 / 3层 |
| 效果 | 60.11% / 58.99% / 57.96% | 59.6% / 59.3% |
ner-crf: 公司数据
| 直接微调 | BERT-of-Theseus | |
|---|---|---|
| 层数 | 完整12层 / 前6层 / 前3层 | 6层 / 3层 |
| 效果 | 97.5% / 97.0% / 96.1% | 97.3% / 96.6% |
可以看到,相比直接那前几层微调,bert-of-theseus的效果确实更好,此外,我还尝试了线性策略的替换概率,效果上差别不大。
实验代码:classification_ifytek_bert_of_theseus
sequence_labeling_ner_bert_of_theseus
