from softmax to crf

from softmax to crf

  • 2019-12-26
  • 次

又做NER相关东西， 用到了CRF，所以想给组里人从头一步一步的将CRF讲一遍，希望大家看完能明白CRF的数学模型已经工程上的使用。
网上关于CRF大多数都是将他与HMM及概率图模型一起对比着讲，但是我觉得这需要一些背景知识，鉴于上次分享发现大家并没有什么背景知识，
所以这次希望能尽量减少背景知识就能让人搞懂CRF。

序列标注

模型

通常CRF出现在序列标注任务中，所以我们先来看看序列标注主要是做什么的。
序列标注是NLP中一个重要的任务，它包括分词、词性标注、命名实体识等。下面用一个分词的例子来简单说明。（原文)
假设我们现在用$bmes$四标签来进行分词，其中b 代表begin即词的开头， m代表middle即词内，e代表end即词的结尾，s代表single即单独成词。
现在我们有一个字符串序列 “今天天气不错”，如果对应的分词结果为“今天/天气/不/错”，则其标签序列为“bebess”。由于在序列标注中，我们认为正确的标签序列是唯一的，
所以我们的目标就是在所有可能的标签序列中（如bbbbbb,ssssss)挑选出真实的标签序列（bebess), 即最大化概率$P(bebess|今天天气不错）$。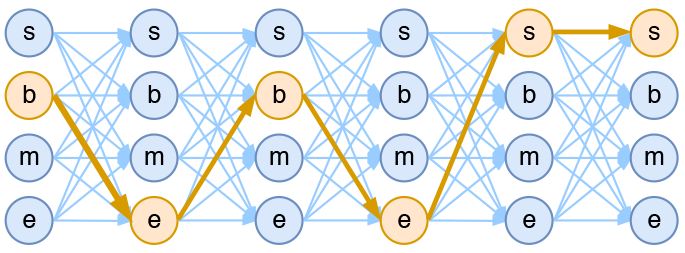
4tag分词网络示意图
即在上图中，所有从左至右的连线中，选出黄色的那条。

数学形式

我们假设输入序列是$X=[x_1, x_2, x_3, …, x_n]$,对应的输出序列是 $Y = [y_1, y_2, …, y_n]$,
label的集合为$L = [l_1, l_2, … , l_k]$. 任务目标是让真实的输出序列的概率最大，即：
$$
Max(P(y_1,y_2,..y_n|X))
$$

沿时间轴Softmax

直接对上述模型进行求解比较困难，所以我们先将问题简化，然后在对简化后的问题进行求解。
首先，我们引入朴素假设：即标签之间独立不相关，对应的目标就简化为：
$$
Max(P(y_1|X)P(y_2|X)…P(y_n|X))
$$
为了对$P(y_i|X)$进行建模，通常我们先通过RNNs（LSTM，BiLSTM, etc)来捕获输入X的全局信息，获得隐藏状态序列$\bar{x_1}, \bar{x_2}, …, \bar{x_n}$,
此时的$\bar{x_i}$可以看作是$x_i$ 通过X获取的特征，由于RNNs可以捕获全局信息，所以我们认为特征$\bar{x_i}$之间互不相关，对应的
$$P(y_i|X) = P(y_i|\bar{x_i})$$
我们的目标：
$$
Max(P(y_1|X)P(y_2|X)…P(y_n|X))
= Max(P(y_1|\bar{x_1})P(y_2|\bar{x_2})..P(y_n|\bar{x_n}))
= Max(\prod(P(y_i|\bar{x_i})))
$$
此时只需要$Max(P(y_i|\bar{x_i}))$进行求解，即沿时间轴一步一步的对RNNs的隐藏输出通过softmax来最大化对应目标标签概率。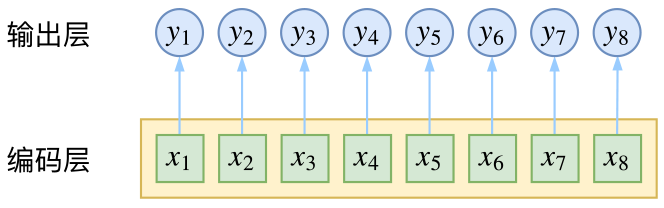
沿时间轴softmax

CRF

因为在上一个方案中，我们做了朴素建设，将输出序列看作是相互独立的一元模型，这样会引入一些问题，如在分词中（bmes），m- 标签不能出现在s- 后面，
s- 标签不能出现在b- 和m-后面等，所以即使在上述方案中，至少也需要人为的设置一个“转移矩阵”，将不合理的转移方式得分置为0，来避免不合理方案的出现。
而上述方案出现错误的原因，本质上是因为我们的朴素假设：标签之间相互独立。为了解决上述方案的问题，我们至少需要在输出端显式考虑标签的关联性，即输出标签与上下文相关。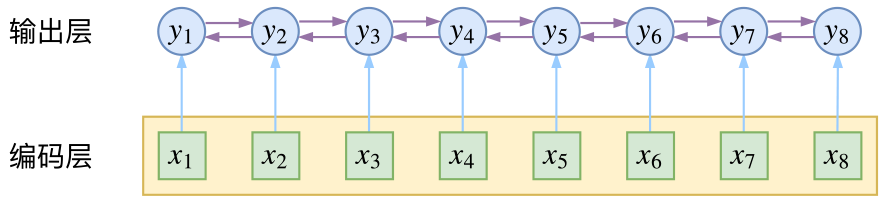
显式考虑输出端上下文
显式考虑输出端上下文相关

现在我们回到原始目标上来，原始目标是$Max(P(y_1,y_2,..y_n|X)) $, 上个方案中我们是因为直接对$P(y_1, y_2,…y_n|x_1, x_2, …,x_n)$直接建模很难，
所以才做出了假设，简化目标。现在让我们换个思路，为了求解上述概率，我们还可以穷举出输出序列所有的可能结果$Y_1, Y_2, …, Y_{k^n}$,
然后如果能计算出当前输入X对应每种可能的输出序列的“值”， 则我们可以通过Softmax计算出真实输出序列的概率，即得到$P(Y_{true}|X)$。
假设一：我们可以学习一个打分函数f，通过函数f可以得到输出序列关于输入的得分，即$score_i = f(Y_i, X)$
此时，我们的目标就转化为 $P(Y|X) = \frac{exp(f(y_1, y_2,…y_n; X))}{Z(X)}$.
其中$Z(X) = \sum_{i=1}^{k^n}(exp(f(Y_i, X)))$。即此时的概率P是一个指数分布。
此时我们的方案是1个$k^n$多分类问题，即我们是对一个完整的输出序列为单位来计算概率（路径积分），而上一个方案中，是n个k分类问题，
这是两个方案的不同点之一。
在方案一中我们也说过，直接对完整序列建模比较困难，此时我们直接对$f(Y_i, X)$求解也会面临相同的困难，为了避免方案一的问题，我们不再使用一元模型，改为二元模型。
引入一阶马尔可夫假设，且其关联性是加性的。即当前输出标签只与前一个输出标签相关，其总得分是对所有得分求和。
此时的目标就转化为
$$
P(y_1, y_2, …, y_n|X)
= P(y_1|X)P(y_2|y_1;X)…P(y_n|y_{n-1}|X)
= P(y_1|X)\frac{P(y_1,y_2|X)}{P(y_1|X)P(y_2|X)} P(y_2|X) … \frac{P(y_{n-1}, y_n|X)}{P(y_{n-1}|X)P(y_n|X)} P(y_n|X)
$$
假设一中我们假设P是一个指数分布，所以此时我们引入两个函数e 和 t：e对$P(y_i|X)$建模, t 对$\frac{P(y_1,y_2|X)}{P(y_1|X)P(y_2|X)}$建模，即：
$$
P(y_i|X) = exp(e(y_i, X))
\frac{P(y_{i-1},y_1|X)}{P(y_{i-1}|X)P(y_i|X)} = P(y_i|X)exp(t(y_{i-i}, y_i; X))
$$

此时的目标就化简为：
$$
P(y_1, y_2, …, y_n|X)
= \frac{exp(f(y_1, y_2,…y_n; X))}{Z(X)}
= \frac{1}{Z(X)} exp(e(y_i,X) + t(y_1, y_2; X) + e(y_2, X) + … + t(y_{n-1}, y_n; X) + e(y_n, X))
$$
此时我们只需要对每个标签和相邻标签打分，然后将所有打分求和，即可得到总得分，然后对目标进行求解。

线性链CRF

虽然上面已经做了大量简化，但是求解时依然比较困难，主要是在求解t中，因为需要同时对输入X与标签$y_i$, $y_{i-1}$同时考虑，而在e中，
已经将输入与输出的关联进行了建模，此时我们引入线性链假设：假设t与输入X无关，则此时$ t(y_{i-1}, y_i;X) = t(y_{i-1}, y_i)$，那打分函数f简化为：
$$
f(y_1, y_2, …, y_n;X)
= e(y_1,X) + t(y_1, y_2) + e(y_2, X) + … + t(y_{n-1},y_n;X) + e(y_n,X)
$$
此时t就是一个待训练的参数矩阵，而e则可以通过RNNs来建模，概率分布也变为：

$$
P(y_1, y_2,…,y_n|x_1, x_2,…,x_n)
= exp(e(y_1, X) + \sum_{i=1}^{n-1}[t(y_i, y_{i+1}) + e(y_{i+1}, X)])) \frac{1}{Z(X)}
$$

求解

为了求解模型，我们用最大似然法， 即：

$$loss = -logP(y_1, y_2, …, y_n|x_1, x_2, …, x_n)$$
将上式代入：

$$loss = logZ(X) - (e(y_1, X) + \sum_{i=1}^{n-1}[t(y_i, y_{i+1}) + e( y_{i+1} , X)]) $$

减号后面的项通过添加一个待训练的参数矩阵循环计算即可得到结果，难算的前面的归一化因子Z(X)。前面我们也说了，我们此时是以路径为单位，
则此时Z(X) 需要我们穷举所有可能的路径比对其打分求和，而此时的路径有 $k^n$条，是指数级的，直接算效率太低，几乎不可能。
在假设二中，我们引入了一阶马尔可夫假设，当前标签只与前一个标签有联系，因此我们可以递归的计算归一化因子，这使得原来是指数级的计算量降低为线性级别。原文
（这点是求解归一化因子的关键，最初我在推导时一直卡在这点上）
具体的: 将计算到时刻t的归一化因子记为Zt，并将它安装标签分为k个部分，即：

$$Zt = Zt^1 + Zt^2 + … + Zt^k$$
其中$Zt^i$表示以标签i为终点的所有路径的得分指数和，此时，我们写出递归公式：

$$Z_{t+1}^1 = (Zt^1 T_{11} + Zt^2 T_{21} + … + Zt^k T_{k1})E_{t+1}(1|X)$$

$$… $$

$$Z_{t+1}^k = (Zt^1 T_{1k} + Zt^2 T{2k} + … + Zt^k T_{kk})E_{t+1}(k|X)$$

其中T是矩阵t的各个元素取指数形式，即$T_{ij} = exp(t_{ij})$, E是e的指数形式，即$E_{ij} = exp(e_{ij})$, 而$e_{ij}$是指时刻i时RNNs对label j的打分。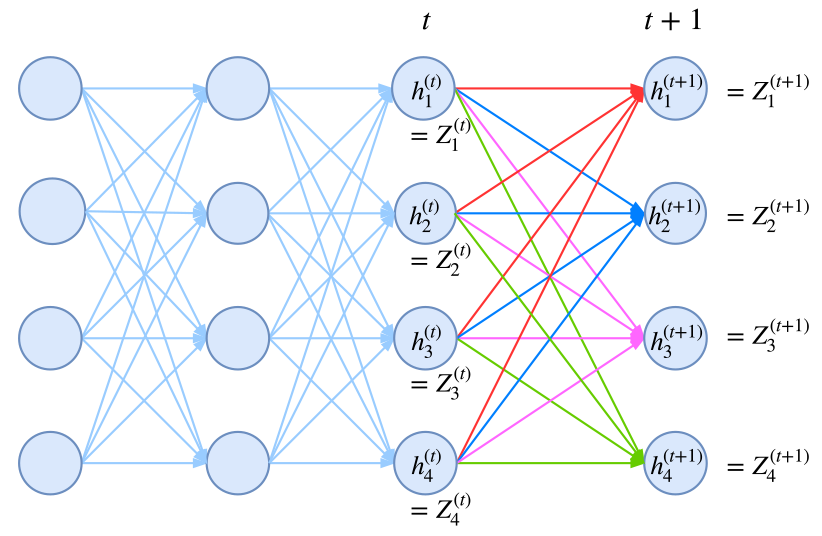
logz

上式带有指数形式，我们取对数来简化计算过程。
$$
log(Z_{t+1}^1) = log((Zt^1 T_{11} + Zt^2 T_{21} + … + Zt^k T_{k1})E_{t+1}(1|X) ) \\
=log(exp(log(Zt^1) + t_{11}) + exp(log(Zt^2) + t_{21}) + … + exp(log(Zt^k) + t_{k1}) exp(e_{t+1}(1|X))) \\
= log(exp(log(Zt^1) + t_{11} + e_{t+1}(1|X)) + exp(log(Zt^2) + t_{21} + e_{t+1}(1|X)) + … + exp(log(Zt^k) + t_{k1} + e_{t+1}(1|X)))\\
= log(\sum_k(log(Zt^k) + t_{k1} + e_{t+1}(1|X)))
$$

上面的过程比较曲折，对有些同学可能不太好理解，我们用一个简单的例子来帮助理解。
我们假设我们现在有一个输入$X=[w_0,w_1, w_2]$, 标签集合为$L=[l_1, l_2]$. RNNs对e完成了建模，即：

 l1l2
w0$e_{01}$$e_{02}$
w1$e_{11}$$e_{12}$
w2$e_{21}$$e_{22}$

其中$e_{ij}$代表第i个字是第j个标签的得分。
转移矩阵t:

 l1l2
l1t11t12
l2t21t22

其中$t_{ij}$代表第i个标签转换为第j个标签的得分。
接下来我们按从$w_0$到$w_2$的方向一步一步来进行计算。首先，我们引入两个变量: states, cur，其中:

  • states代表上一个时刻计算的最终结果，即对应$log(Z_t^i)$

  • cur代表当前时刻各个标签的得分，即对应$e_t^i$

  • $w_0$:

  • states = None
  • $cur = [e_{01}, e_{02}]$
    此时:
    $$log(Z) = exp(e_{01}) + exp(e_{02})$$
  • $w_0$ –> $w_1$:
  • states = $[e_{01}, e_{02}]$
  • cur = $[e_{11}, e{12}]$
  1. 扩展states:
    $
    states = $$\begin{pmatrix}
    e_{01}&e_{01}\\
    e_{02}&e_{02}\\
    \end{pmatrix}$$
    $
  1. 扩展cur:
    $
    cur = $$\begin{pmatrix}
    e_{11}&e_{12}\\
    e_{11}&e_{12}\\
    \end{pmatrix}$$
    $
  1. 将cur, states 与转移矩阵t 求和:

$
score = $$\begin{pmatrix}
e_{11}&e_{12}\\
e_{11}&e_{12}\\
\end{pmatrix}$$
$+$ $$\begin{pmatrix}
e_{01}&e_{01}\\
e_{02}&e_{02}\\
\end{pmatrix}$$
$+$ $$\begin{pmatrix}
t_{11}&t_{12}\\
t_{21}&t_{22}\\
\end{pmatrix}$$
$=$ $$\begin{pmatrix}
e_{01} + e_{11} + t_{11} & e_{01} + e_{12} + t_{12}\\
e_{02} + e_{11} + t_{21} & e_{02} + e_{12} + t_{22}\\
\end{pmatrix}$$
$

  1. 对score取指数形式然后求和，得到新的states:
    $$
    states = [log(exp(e_{01} + e_{11} + t_{11}) + exp(e_{02} + e_{11} + t_{21})), log(exp(e_{01} + e_{12} + t_{12}) + exp(e_{02} + e_{12} + t_{22}))]
    $$
    其中，states中的每个元素即对应着式中$logZ_{t}^i$, 此时的$log(Z)= \sum_k(exp(log(Z^k)))$:

$$
log(Z_{0,1}) = log(exp(log(exp(e_{01} + e_{11} + t_{11}) + exp(e_{02} + e_{11} + t_{21}))) + exp(log(exp(e_{01} + e_{12} + t_{12}) + exp(e_{02} + e_{12} + t_{22})))) \\
= log(exp(e_{01} + e_{11} + t_{11}) + exp(e_{02} + e_{11} + t_{21}) + exp(e_{01} + e_{12} + t_{12}) + exp(e_{02} + e_{12} + t_{22}))
$$

当序列长度为2，标签有两个时，所有可能的标签序列为$(label_1->label_1, label_2->label_1, label_1->label_2, label_2->label_2)$,而对应的序列得分，即对应上式中的项，即：

  • $ S_1: label_1->label_1:$
    $ S_1 = e_{01} + e_{11} + t_{11} $
  • $S_2: label_2->label_1:$
    $ S_2 = e_{02} + e_{11} + t_{21}$
  • $S_3 = label_1->label_2:$
    $ S_3 = e_{01} + e_{12} + t_{12}$
  • $S_4 = label_2->label_2:$
    $ S_4 = e_{02} + e_{12} + t_{22}$
  • $w_0$ -> $w_1$ -> $w_2$:
  • $states = [log(exp(e_{01} + e_{11} + t_{11}) + exp(e_{02} + e_{11} + t_{21})), log(exp(e_{01} + e_{12} + t_{12}) + exp(e_{02} + e_{12} + t_{22}))] $
  • $cur = [e_{21}, e_{22}]$

与上面的做法一样，也分为4步：

  1. 扩展states:
    $
    states = $$\begin{pmatrix}
    log(exp(e_{01} + e_{11} + t_{11}) + exp(e_{02} + e_{11} + t_{21}))&log(exp(e_{01} + e_{11} + t_{11}) + exp(e_{02} + e_{11} + t_{21}))\\
    log(exp(e_{01} + e_{12} + t_{12}) + exp(e_{02} + e_{12} + t_{22}))&log(exp(e_{01} + e_{12} + t_{12}) + exp(e_{02} + e_{12} + t_{22}))\\
    \end{pmatrix}$$
    $
  1. cur：
    $
    cur = $$\begin{pmatrix}
    e_{21} &e_{22}\\
    e_{21} &e_{22}\\
    \end{pmatrix}$$
    $
  1. 将states，cur与转义矩阵t求和：

$$
scores = \begin{pmatrix}
log(exp(e_{01}+e_{11}+t_{11}) + exp(e_{02}+e_{11}+t_{21})) & log(exp(e_{01}+e_{11}+t_{11}) + exp(e_{02}+e_{11}+t_{21})) \\
log(exp(e_{01}+e_{12}+t_{12}) + exp(e_{02}+e_{12}+t_{22})) & log(exp(e_{01}+e_{12}+t_{12}) + exp(e_{02}+e_{12}+t_{22}))\\
\end{pmatrix} \\+
\begin{pmatrix}
e_{21} &e_{22}\\
e_{21} &e_{22}\\
\end{pmatrix} \\+
\begin{pmatrix}
t_{11}& t_{12}\\
t_{21}&t_{22}\\
\end{pmatrix} \\=
\begin{pmatrix}
log(exp(e_{01}+e_{11}+t_{11}) + exp(e_{02}+e_{11}+t_{21})) + e_{21} + t_{11} &log(exp(e_{01}+e_{11}+t_{11}) + exp(e_{02}+e_{11}+t_{21})) + e_{22} + t_{12}\\
log(exp(e_{01}+e_{12}+t_{12}) + exp(e_{02}+e_{12}+t_{22})) + e_{21} + t_{21} &log(exp(e_{01}+e_{12}+t_{12}) + exp(e_{02}+x_{12}+t_{22})) + e_{22} + t_{22}\\
\end{pmatrix}
$$

  1. 对score取指数形式然后求和，得到新的states:

$$ states = [\\
log(exp(log(exp(e_{01}+e_{11}+t_{11}) + exp(e_{02}+e_{11}+t_{21})) + e_{21} + t_{11})+exp(log(exp(e_{01}+e_{12}+t_{12}) + exp(e_{02}+e_{12}+t_{22})) + e_{21} + t_{21})), \\
log(exp(log(exp(e_{01}+e_{11}+t_{11}) + exp(e_{02}+e_{11}+t_{21})) + e_{22} + t_{12})+ exp(log(exp(e_{01}+e_{12}+t_{12}) + exp(e_{02}+x_{12}+t_{22})) + e_{22} + t_{22})))] \\
= [log((exp(e_{01}+e_{11}+t_{11}) + exp(e_{02}+e_{11}+t_{21}))exp(e_{21} + t_{11}) + (exp(e_{01}+e_{12}+t_{12}) + exp(e_{02}+e_{12}+t_{22}))exp(e_{21}+t_{21})),\\
log((exp(e_{01}+e_{11}+t_{11}) + exp(e_{02}+e_{11}+t_{21}))exp(e_{22} + t_{12}) + (exp(e_{01}+e_{12}+t_{12}) + exp(e_{02}+e_{12}+t_{22}))exp(e_{22}+t_{22}))]
$$

现在，我们用states计算一下$(Z_2)$:

$$
log(Z_{(0->1->2)}) = log(exp(states[0]) + exp(states[1])) \\
=log((exp(e_{01}+e_{11}+t_{11}) + exp(e_{02}+e_{11}+t_{21}))exp(e_{21} + t_{11}) + (exp(e_{01}+e_{12}+t_{12}) + exp(e_{02}+e_{12}+t_{22}))exp(e_{21}+t_{21})) \\+
log((exp(e_{01}+e_{11}+t_{11}) + exp(e_{02}+e_{11}+t_{21}))exp(e_{22} + t_{12}) + (exp(e_{01}+e_{12}+t_{12}) + exp(e_{02}+e_{12}+t_{22}))exp(e_{22}+t_{22})) \\
= log(exp(e_{01}+e_{11}+t_{11}+e_{21}+t_{11}) + exp(e_{02}+e_{11}+t_{21}+e_{21}+t_{11}) \\ +
exp(e_{01}+e_{12}+t_{12} +e_{21}+t_{21}) + exp(e_{02}+e_{12}+t_{22}+e_{21}+t_{21}) \\+
exp(e_{01}+e_{11}+t_{11} +e_{22}+t_{12}) + exp(e_{01}+e_{11}+t_{11}+e_{22}+t_{12}) \\+
exp(e_{01}+e_{12}+t_{12} +e_{22}+t_{22}) + exp(e_{01}+e_{12}+t_{12}+e_{22}+t_{21}))
$$

上式也就是我们要求的最终结果$log(Z)$,其中指数内对应着所有路径的得分。
到此，上例中的整个归一化因子的计算过程也就完成了，而CRF中最难的部分也就解决了。

demo

搞懂了理论部分，下面写一个demo来验证一下。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
class CRF(Layer):
    def __init__(self, mask_label=False, **kwargs):
        self.mask_label = 1 if mask_label else 0
        super(CRF, self).__init__(**kwargs)

    def build(self, input_shape):
        self.num_label = input_shape[-1] - self.mask_label
        self.trans = self.add_weight(name='crf_trans',
                                     shape=(self.num_label, self.num_label),
                                     trainable=True,
                                     initializer='glorot_uniform')

    def path_score(self, inputs, labels):
        '''
        :param inputs: (batch_size, timesteps, num_label), obtained from rnn(lstm, bilstm. etc.)
        :param labels: one-hot, (batch_size, timesteps, num_label) , real target series
        :return:  path score
        '''
        point_score = K.sum(K.sum(inputs * labels, 2), 1, keepdims=True)
        label_pre = K.expand_dims(labels[:, :-1], 3)
        label_next = K.expand_dims(labels[:, 1:], 2)
        label_trans = label_pre * label_next
        trans = K.expand_dims(K.expand_dims(self.trans, 0), 0)
        trans_score = K.sum(K.sum(label_trans * trans, [2, 3]), 1, keepdims=True)
        return point_score + trans_score

    def log_norm_pre(self, inputs, states):
        '''
        expand previous states and inputs, sum with trans
        :param inputs: (batch_size, num_label), current word emission scores
        :param states: (batch_size, num_label), all paths  score of previous word
        :return:
        '''
        states = K.expand_dims(states[0], 2)
        inputs = K.expand_dims(inputs, 1)
        trans = K.expand_dims(self.trans, 0)
        scores = states + trans + inputs
        output = K.logsumexp(scores, 1)
        return output, [output]
        # states = K.expand_dims(states[0], 2)  # (batch_size, output_dim, 1)
        # trans = K.expand_dims(self.trans, 0)  # (1, output_dim, output_dim)
        # output = K.logsumexp(states + trans, 1)  # (batch_size, output_dim)
        # return output + inputs, [output + inputs]

    def loss(self, y_true, y_pre):
        '''
        :param inputs: (batch_size, timesteps, num_label)
        :return:
        '''
        # mask = 1 - y_true[:, 1: -1] if self.mask_label else None
        # # y_true, y_pred = y_true[:, :, :self.num_label], y_pre[:, :, :self.num_label]
        # real_path_score = self.path_score(y_pre, y_true)
        # init_states = [y_pre[:, 0]]
        # log_norm, _ = K.rnn(self.log_norm_pre, initial_states=init_states, inputs=y_pre[:, 1:], mask=mask)  # log(Z)
        # log_norm_score = K.logsumexp(log_norm, 1, keepdims=True)
        # return log_norm_score - real_path_score
        mask = 1 - y_true[:, 1:, -1] if self.mask_label else None
        y_true, y_pre = y_true[:, :, :self.num_label], y_pre[:, :, :self.num_label]
        init_states = [y_pre[:, 0]]  # 初始状态
        log_norm, _, _ = K.rnn(self.log_norm_pre, y_pre[:, 1:], init_states, mask=mask)  # 计算Z向量（对数）
        log_norm = K.logsumexp(log_norm, 1, keepdims=True)  # 计算Z（对数）
        path_score = self.path_score(y_pre, y_true)  # 计算分子（对数）
        return log_norm - path_score  # 即log(分子/分母)

    def call(self, inputs):  # crf 只是loss，不改变inputs
        return inputs

    def accuracy(self, y_true, y_pred):
        mask = 1 - y_true[:, :, -1] if self.mask_label else None
        y_true, y_pred = y_true[:, :, :self.num_label], y_pred[:, :, :self.num_label]
        isequal = K.equal(K.argmax(y_true, 2), K.argmax(y_pred, 2))
        isequal = K.cast(isequal, 'float32')
        if mask == None:
            return K.mean(isequal)
        else:
            return K.sum(isequal * mask) / K.sum(mask)

结果：
result

关于头图

初雪下的红果果

如果觉得这篇文章不错，对你有帮助，欢迎打赏一杯蜜雪冰城。

logo
分享一个有趣的游戏
Backup