
词向量总结
异同
本文主要讨论Glove和word2vec两种模型对应词向量。
相同点
- 两种模型都是在对词对的
PMI做分解,所以他们具有相同的性质(向量可加性,点积,余弦距离,模长等)。 - 模型的基本形式都是向量的点积,且都有两套词向量空间(单词向量空间与上下文词向量空间)。
不同点
- 1.通常我们都是根据模型来推导其对应性质,而Glove是通过其性质来反推模型,这种方式还是给人眼前一亮的。
- 2.除Glove以外的词向量模型都是对条件概率$P(w|context)$进行建模,如
word2vec的SkipGram对$P(w_2|w_1)$进行建模,但是这个信息是有缺点的,首先,他不是一个严格对称的模型,即$P(w_2|w_1)$ 与 $P(w_1|w_2)$ 并不一定相等,所以,在建模时需要把上下文与中心词向量区分开,不能放到同一个向量空间;其次,这个概率是有界的、归一化的量,所以在模型里需要用softmax等对结果进行归一化,这个也会造成优化上的困难。而Glove可以看作是对$PMI$进行建模,而$PMI$是比概率更对称也更重要的一个量。 - 3.如Glove论文中所述,就整体目标函数而言,可以看作是两种模型采用了不同的损失函数,其基本形式是一致的。
- 4.两种模型都是词袋模型(一元模型)。
- 5.对应词向量内积含义不同:
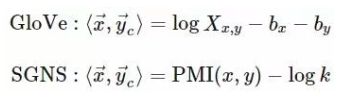
性质
PMI角度
上文说了两种模型都是对词对的PMI做分解,所以我们在解释其性质时直接从PMI的角度来解释。
首先来看一下PMI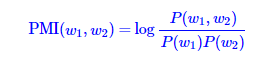
对于任意两个词序列Q和A,其中$Q=(q1,q2…qk)$, $A = (a1, a2…al)$,我们模型都是采用的词袋模型,即满足朴素假设:每个特征之间相互独立。
带入朴素假设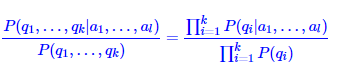
用贝叶斯公式变换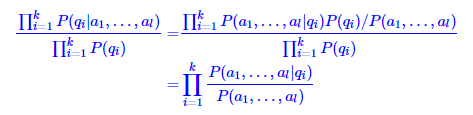
再用一次朴素假设
最后得到: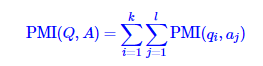
即在朴素假设下,两个序列的互信息等于两个序列中各个项的互信息的总和。
可加性
在Glove和word2vec中,两个词之间的相关性是通过对应词向量的内积来表达的,即对于词$W_i$, $W_j$, 其相关性等于$<V_i ,V_j>$, 带入上面,即: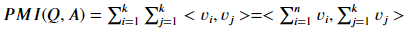
即两个词序列的相关性可以通过将两个序列内的词向量求和后再进行点积计算。
如我们求两个句子的相关度时,可以先将句子内的词对应的词向量进行求和,然后再进行相似性计算。
模长
词向量w的模长正比与其内积<w,w>,即正比PMI(w,w),而在一个滑动窗口内,上下文中的词与中心词相等的概率极低,所以可以认为P(w,w) ~ P(w),推出
即,模长正比与词频的倒数,词频越高(停用词,虚词等),其对应的模长越短,这样就表面模长能在一定程度上代表词本身的重要性。
从模型学习的角度来看,词向量的内积等于其模长的乘积乘以余弦值,即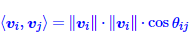
对于高频的几乎没有什么固定搭配的词,其所含语义也相对非常少,即这些词与其他任意词的互信息都非常低,约等于0,而为了让上式等于0,与其不停的调节两个向量的方向,不如让其中一个的模长像0靠近,这样经过多次迭代后,高频的语义少的词的模长就越来越短,逐渐接近0.
实验结果中,也能看到按模长排序后,前面的都是高频的语义含量极低的词。
可以看到,排在前面的都是高频的语义极少的词(’UNK’,’以及’,’三’,符号等)
相关性
两个词的互信息正比于词对应向量的内积,即两个词互信息越大,两个词成对出现的几率越高,其对应词向量的内积也就越大,因此,可以通过内积来对词的相关性进行排序。而上面也说了,模长代表了词的重要程度,如果我们不考虑词本身的重要程度,只考虑其词义,可以用向量范数将其归一化后在进行内积计算,这样更稳定.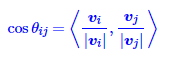
即词的相关性可以用词向量之间的余弦距离来计算,这样比只使用内积更稳定。
在统计上,互信息为0,则表面这两个词无关,对应到模型,即两个词的词向量的内积为0,而根据向量的知识,两个向量的内积为0,则表明两个向量相互垂直,即两个向量无关。两个词在统计上的无关正好对应其在词向量空间上的几何无关!
应用
两个句子的相关性
计算两个句子或短语之间的相关性时,我们可以借鉴上面PMI在朴素假设下的性质,将两个句子中的词向量进行求和,再计算两个结果向量之间的相关性,如点积或余弦。
而如果一个句子内的词向量的和与某一个词的词向量相关性非常高,可以认为这个句子与这个词表达了相同的语义,或者,在词向量空间内,词对应的向量在句子的聚类中心附近。
中心词(关键词)提取
所谓中心词(关键词),即能概况句子的意思,通过这些词,我就能大概猜到整个句子的整体内容。即这些词(相对句子内其他词)对整个句子的相关性更高。这样就能将问题转化成词与句子相关性排序问题。
通过语言模型的角度来看,语言模型本身就是一个通过上(下)文来预测下一个词概率的模型,即最大化$P(w1,w2,w3..|W)$.而关键词的含义是什么呢?用数学的方式表达就是:
对于$S=(w1,w2, w3..wk)$,求解$P(S|wk)$值最高的$wk$,其中$wk$属于$S$。这其实与语言模型的含义是一致的。
最终,将问题转化成词与句子之间的相关性排序问题,而上面提到求解两个句子相关性时,可以将句子对应词向量先求和再计算相关性,最后关键词提取就变成:
先将句子对应词向量求和,得到sen_vec,然后计算单个词与sen_vec的相关性,然后排序即可。
可以看到结果还是相当不错的。
句向量
上面在做句子相关性时,都是为了将计算从$O(n^2)$降低到$O(n)$而将句子内的词向量进行求和,然后再计算。其实也就是用词向量的求和来得到句向量,来作为句子在相同词向量空间的语义。其实这是一种简单又快捷的得到句向量的方式,在很多任务中都可以尝试使用。
refer
neural-word-embedding-as-implicit-matrix-factorization
https://aclweb.org/anthology/P17-1007
关于头图
摄于秦皇岛
