深入谈谈word2vec

小蛋子

2019-10-21

Word2vec

NNLM复杂度
优化方案
- 1.Hierarchical softmax
- 2.negative sampling
四种训练方案
思考
回答
关于头图

NNLM复杂度

原始的NNLM在训练词向量时非常耗时，尤其是大规模语料上，作者在论文后也提出了可能的优化方案，所以word2vec的关注点就是如果更加有效的在大规模语料上训练词向量。
每个训练样本的计算复杂度：
$$
Q = N * D + N * D * H + H * V
$$
其中V是词典大小，每个词编码为1-of-V，N是当前序列中当前词的前N个词，D是词向量大小，H是神经网络层中隐层神经元个数。
这个$Q$中的主要部分是最后的$H * V$ 部分，但通过一些优化方法可以降低（hs/ng), 所以此时的主要的复杂度来着 $N * D * H$, 所以作者直接将神经网络层去掉，来提高计算效率。
作者之前的工作发现成功的训练一个神经网络语言模型可以通过两步进行：1，首先通过一个简单模型训练词向量，2，然后在这之上训练N-gram NNLM。同时，增加当前词后续的词（下文信息）可以得到更好的结果。基于此，提出了两种结构的模型：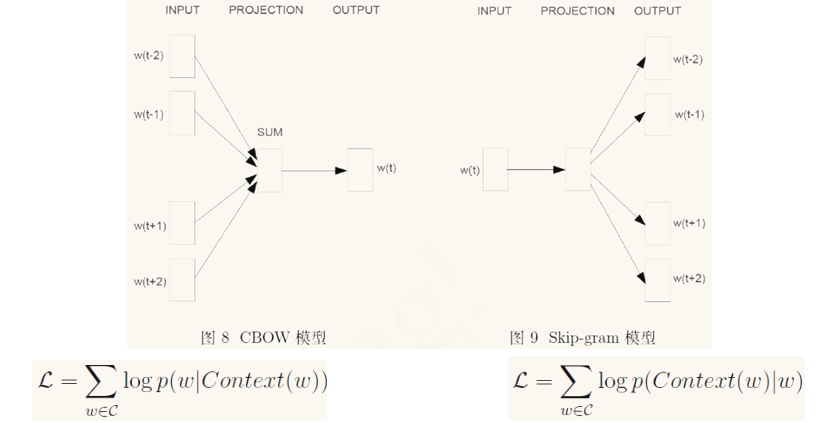
CBOW vs Skip-gram

1.CBOW：与NNLM类似，但是将网络层去掉，同时使用当前词的下文，即通过将上下文窗口内的词投影得到统一向量，然后预测当前词。此时模型内词的顺序不再影响投影结果，计算复杂度为：$Q = N * D + D * log(V)$
2.Skip-gram: 与CBOW类似，不过是通过当前此来预测上下文内的词，为了提高效率，在实际工程上对上下文内的词进行了采样，此时的计算复杂度为：$Q = C * (D + D * log(V))$

优化方案

之前提到原始NNLM中的主要计算复杂度是输出层，即 $H * V$，主要的优化思路是避免全量计算V的概率，作者实现了两种方案，即 Hierarchical Softmax 和negative sampling

1.Hierarchical softmax

通过词频构建霍夫曼树，然后将输出层用霍夫曼树替换，上一层结果与每个节点做二分类，判断属于词类，叶子节点为对应的词，判断属于该词的概率

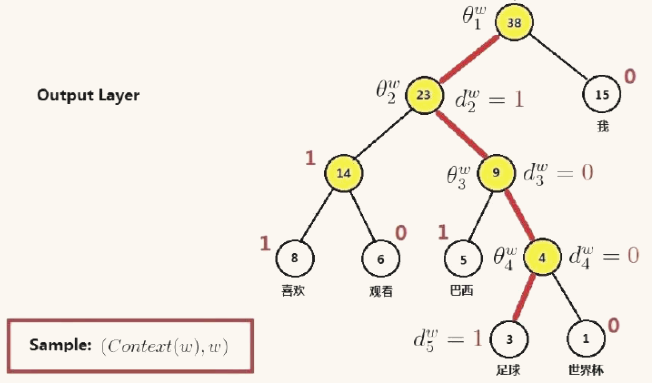
特点：高频词的位置更靠近根节点，所需的计算进一步降低。但对于低频词，其对应位置远离根，对应路径长，所需计算量依然很大，效率不高

2.negative sampling

在输出层避免对全量字典进行判断，而通过先验知识来圈出最容易混淆的一部分，然后组成负样本（相对于当前词）。作者提出通过词频来归一化后的比例来组成一定比例的候选集，随机的在候选集选取一定数量的负样本(n << V)来组成负样本集，最后的softmax多分类层变成多个sigmod二分类层，来提高计算效率及词向量的质量。

四种训练方案

1.基于hs的CBOW

其中

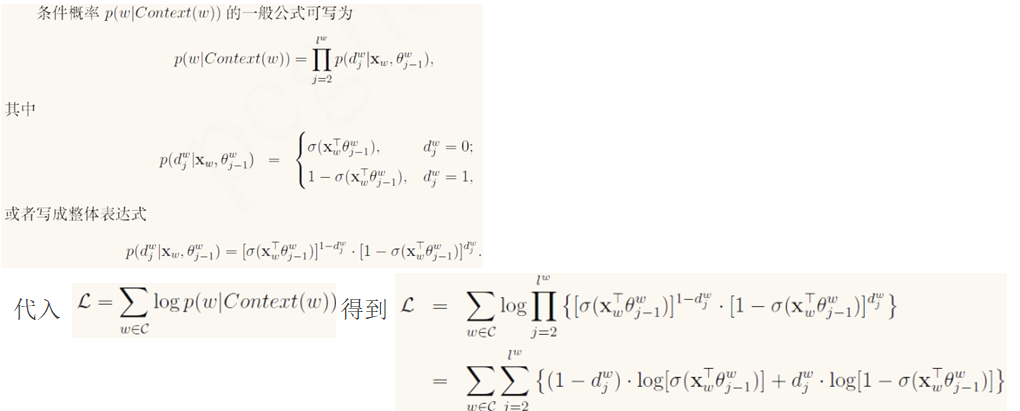
对应的伪代码：

2.基于hs的Skip-gram

对应的伪代码：

3.基于ng的CBOW

对应伪代码：

4.基于hs的skip-gram

G中表达式与基于hs的CBOW一样，只是在最外面多了一层求和，后面的过程与CBOW一样。

思考

1.词向量的训练过程是一个fake task，我们的目标不是最后的语言模型，而是在这个过程中产生的feature vector，用一个real task 来训练是不是更好？
2.因为是个fake task，那我们如何评估这个task，又如何评估得到的词向量的质量？论文中使用了近似词对及线性平移的特性，有没有更好的方式？
3.词向量的“similarity”具体是什么含义？

回答

1.用real task来训练一般会得到更好的词向量，但一般下游任务都是在词向量之上构建，所以一般情况是训练一个词向量，然后作为embedding层的初始参数进行下游任务的训练。
2.除了相似词及线性平移性，其他情况下可以通过下游任务的效率来评估。
3.词向量的“similarity”跟通常意义的近义词或相似词有本质上的区别，词向量更多的含义是“同位词”，即上下文相近的词。换个角度，我们将模型的连接函数形式写出来：

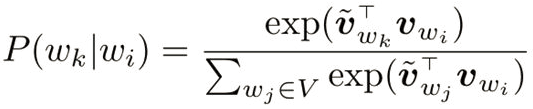
上式中v分别对应左右两个词向量空间的词向量，由于模型是对称的，所以实际使用时左右两个词向量可以任选一个。

其中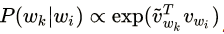

分母是归一化项，暂时忽略，最终最大化$P(w_k|w_i)$的同时，即让 Vwk与 Vwi的内积更大。即模型内隐式的用词向量的内积（方向）来表示词向量直接的距离远近（语义距离），所以可以利用词向量的cosine来寻找语义更接近的词。进一步的，左右两个词向量分属不同的向量空间，最小化两个词的语义距离被转化为最小化两个词在不同语义空间的距离，而不是在同一个向量空间，为什么这种方案可行？原文里提到是因为放在同一个向量空间（同一个矩阵），两个词向量正交在一起，不好优化，，分开放在两个向量空间更利于优化。两个词向量空间为什么可行？我认为主要是因为模型是对称的，虽然两个向量空间不同，但是可以认为是只是经过了旋转缩放，词在向量空间的相对位置没有发生改变（词向量之间的角度）。

优点：

1.没有神经网络层，所以没有耗时的矩阵相乘，只保留了一个softmax层，计算效率高。
2.优化时使用的是随机梯度下降，罕见词不会主导优化目标
demo：https://github.com/xv44586/Papers/blob/master/NLP/WordVector/word2vecDemo.ipynb

论文
https://arxiv.org/pdf/1301.3781.pdf
https://arxiv.org/abs/1310.4546