一、整体思路

获取词向量基本上有两种思路：

• 1.利用全局统计信息，进行矩阵分解（如LSA）来获取词向量，这样获得的词向量往往在词相似性任务上表现不好，表明这是一个次优的向量空间结构；
• 2.利用局部上下文窗口单独训练，但是统计信息作为有用的先验知识，没有很好的利用到。

Glove：结合两种训练方式，获取更好的词向量

二、基本假设

词的共现次数与其语义的相关性往往不是严格成比例，所以直接用共线性来表征词之间相关性效果不好，因此，作者通过引入第三个词，通过词之间的差异来刻画相关性。差异选择用两个词与同一个词的共现概率的次数来更好的判断词之间的相关性。比率：$ratio_{i,j,k}=\frac{Pi,k}{Pj,k} $
看下面这个例子：

ice 与solid相关性高，而steam与solid相关性弱，对应比例大于1；ice与gas相关性弱，steam与gas相关性高，对应比例小于1，ice与steam都与water相关，对应比例约等于1，ice与steam与fashion都不相关，对应比例也是约等于1.
相关性的规律：

三、模型

模型的数学形式为：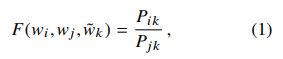

其中$w_i$, $w_j$ 与$w_k$分属不同的两个词向量空间（参考skipgram），对于F函数，我们希望他能够在向量空间内预测$p(P_{ik}/P_{jk})$这个比率，由于向量空间的线性结构，最自然的方式就是用向量的差，即：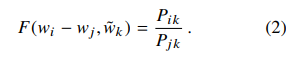

等式的右侧是一个标量，左侧F函数可以是一个复杂函数，而我们上面提到我们希望捕捉向量的线性结构，所以避免使用复杂函数，首先将参数做内积：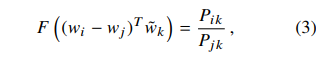

在窗口滑动的过程中，中心词与上下文词的角色会相互转化，但是当词的位置互换后，其相关性应该是保持一致的，所以，F函数需要对和操作与商操作上同态（这里同态的意思是F函数在左右两侧应该是一致的，也就是 $F((w_i - w_j)）= F(w_i) / F(w_j)$：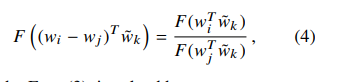

其中：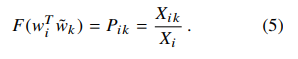

为了解决 上式4，F函数的形式就是exp(指数形式），最终求解后：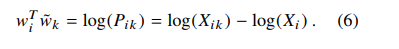

上式中，等式左侧是对称的，即$W_i^T*W_j = W_j^T*W_i$, 而右侧是不对称的，即$log(p_{ij}) != log(P_{ji})$. 如果上式的右侧没有$log(x_i)$,则等式的左右就对称了，考虑到与$k$无关，所以把这一项并入到$i$的偏差项中，即：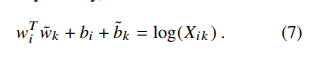

由于上式中有$log$，所以需要处理0值，同时，对于低频与高频的共线词都不能过度训练，于是，优化目标就变成了：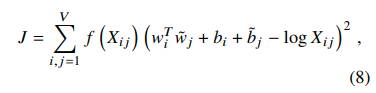

其中，权重函数$f(x)$需要满足：

• 1， f(0)=0
• 2, 非减以避免低频共现过度训练
• 3，抑制高频共现避免过度训练
  最后采用的$f(x)$ 形式为：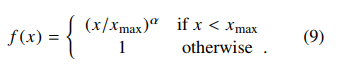
  
  实验中他们采用的是xmax=100, a=3/4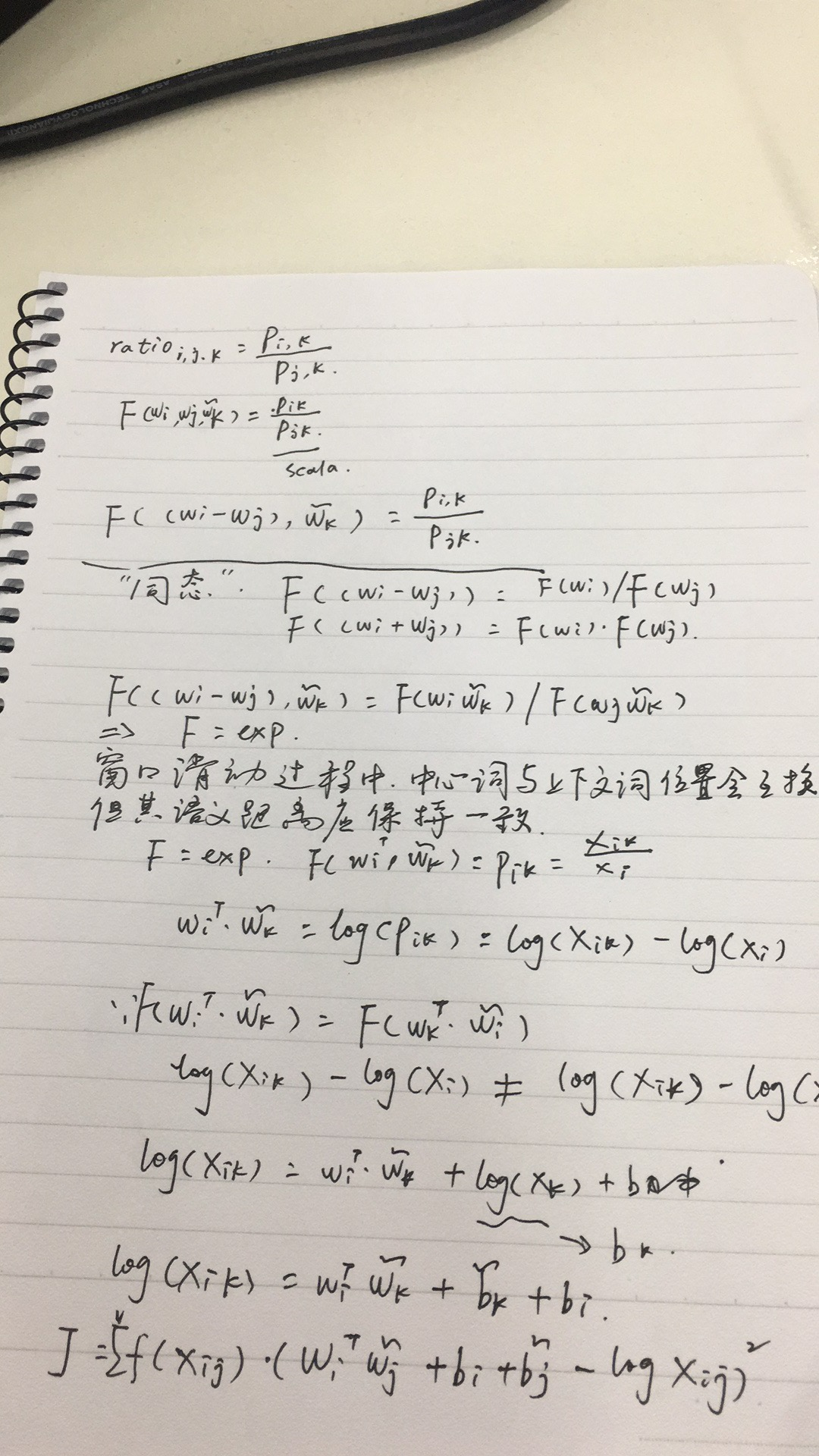
  

四、对比

与局部窗口方式对比：

优化目标使用不同的损失函数，并带有调和函数来降低高频词的影响。
语义相似性结果对比：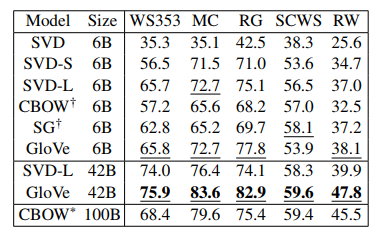

五、思考

• 1.相对与word2vec, Glove引入了词频统计信息，这是很重要的全局信息。
• 2.word2vec的训练次数与词频相关，Glove的训练中词频是loss的weight，高频低频词的overweight的情况更低。
• 3.将基于局部窗口的模型中，相同词进行合并，修改对应object：
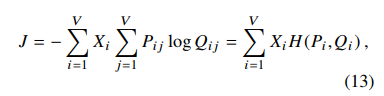
  其中$H$为交叉熵，相对Glove的object：
  
  loss由交叉熵改为最小二乘，$X_i$改为$f(X_i)$函数进行调和。
• 4.Glove中的左右词向量也是两个不同的词向量空间，与word2vec一样，虽然Glove模型上看上去可以使用同一个词向量空间做，但是作者说是因为更好优化且模型更稳定，不同的时，最后的结果是左右词向量求和（虽然word2vec也可以这么做）

Demo:https://github.com/xv44586/Papers/blob/master/NLP/WordVector/GloveDemo.ipynb

再思考：

• 1.通常我们都是根据模型来推导其对应的性质，而Glove是因为其应该具有的性质，来反推模型，这种方式也给人提供了一种新思路。
• 2.为什么两种模型都有两套词向量空间（中心词向量和上下文词向量）？虽然两个作者都说是因为更好优化且模型更稳定，那有没有更合理的理论上的解释呢？我的理解是：对于word2vec，模型直接对概率$p(w|context)$,如skipgram中，直接对$P(w_2|w_1)$进行建模，而$P(w_2|w_1$)与$P(w_1|w_2)$并不一定相等，所以需要针对词的位置区分，也就是需要两套不一样的词向量空间；而Glove中，如上文中公式（6）所示，模型右侧有一个与位置有关的参数，虽然通过引入两个bias可以一定程度上消除这个位置相关的参数，但是这个参数并不是均匀分布，所以仅通过bias不能完全解决这个问题，而引入两个不同的词向量空间，相当于是引入了位置信息，这样能更好的解决这个问题。其最本质的原因是在窗口滑动过程中，词位置变化的同时信息可能是不对称的，即以a为中心词的窗口中的b在以b为窗口时，a可能丢失。
• 3.对于上式8，存在一个比较严重的问题，模型为了消去位置相关参数，将其吸收进bias内，而这个bias的引入，就导致了一个严重的问题，即模型不适定。
  
  即当你求得一组解后，你可以给这组解加上一个常数向量，其还是一组解。那这个问题就很严重了，你无法评估你得到的解是哪组解。如果加上的是非常大的常数向量，那这组词向量在很多度量上就失去了意义（如余弦距离）

  关于头图

  摄于北京某水库

Buy me a coffee

如果觉得这篇文章不错，对你有帮助，欢迎打赏一杯蜜雪冰城。