Dropout--深度神经网络中的Bagging

Dropout--深度神经网络中的Bagging

  • 2019-10-17
  • 次

深度神经网络过拟合问题

深度神经网络由于其巨大的参数量，可以很方便的拟合非常复杂的非线性关系，同时，巨大的参数量也给模型带来了过拟合的问题。为了解决这个问题，也有人提出了早停和加入正则项等手段。而在传统机器学习中，除了这些手段，还有一种手段来解决这个问题，即bagging（参考我之前的文章Bagging为什么能降低过拟合），最典型的就是随机森林：对样本和特征进行抽样，训练多个模型，然后进行集成（投票/求平均）。那如何将这种思路引入到深度神经网络中呢？
首先,由于训练单个深度神经网络就已经非常耗时，通常样本量也不够多，不适合采样，所以像随机森林一样抽样训练多个模型的方案不可取。
剩下的思路就是用“一个”模型来模拟多个sub-model，那如何来模拟呢？

Dropout

对于深度神经网络，其最重要的部分就是其隐藏单元（神经元），对于一个有n个神经元的层，我们可以通过设置神经元是否激活，来模拟$2^n$ 种结构，即sub-model，而在evaluate阶段，我们将这些所有的sub-mdoel的结果进行求平均。那对于现在的结构，不可能对 $2^n$中结构都去做计算然后再求平均，一种近似的做法是用当前这“一个”模型来近似模拟：设置所有神经元都处于激活状态，同时，对每个神经元的输出乘以其激活概率keep_prob.这就是Dropout的背后思想。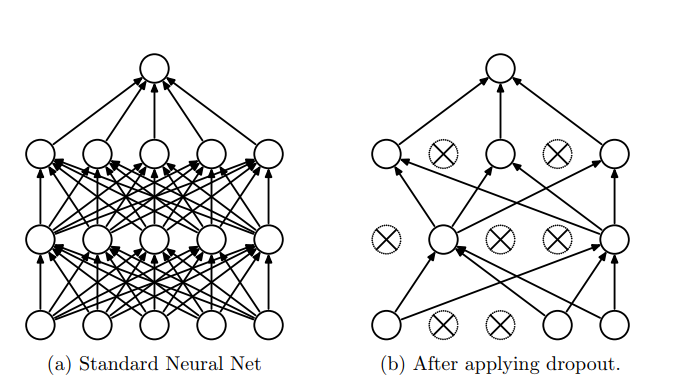
Dropout
简单总结Dropout的具体做法：训练阶段，在前向传播的时候，让某个神经元的激活值以一定的概率p停止工作；预测阶段，对每个神经元的输出乘以1-p (keep_prob)。
接下来思考一下，为什么这么做work:首先，训练阶段部分神经元失活，对应的结果是部分features不参与计算，本质上是对features进行采样；其次，从整个训练过程中看，每次训练（batch-data),都对应不同的失活神经元（sub-model)，对应的每个sub-model在单个epoch内，都是在对样本进行无放回的抽样，本质上是在bagging。最后，在预测阶段，为什么可以用“一个”完整的模型来模拟sub-model的求平均过程呢？从sub-model的角度看，每个sub-model被training的概率为$(1-p)$, 而神经元对所有sub-model是共享的，唯一的区别是是否激活，所以归一到每个神经元上，单个神经元被training（激活）的概率为$(1-p)$,而sub-model的总数是$2^n$，每个神经元求平均的过程即$Out_i * (1-p) * 2^n/ 2^n = Out_i * (1 -p)$.
具体实现时，我们的目的是在训练阶段对神经元进行随机（概率p)失活,而在test和evaluate时，对神经元的输出乘以$(1-p)$,所以在实现时，可以采用一个trick：dropout时，对样本进行mask的同时，将其除以$(1-p)$,这样就可以一次计算完成所有逻辑，同时，把所有逻辑保留在整个层中。
tf的实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
def dropout(x, keep_prob, noise_shape=None, seed=None, name=None):  # pylint: disable=invalid-name
  """Computes dropout.

  With probability `keep_prob`, outputs the input element scaled up by
  `1 / keep_prob`, otherwise outputs `0`.  The scaling is so that the expected
  sum is unchanged.
    ...
 """
  with ops.name_scope(name, "dropout", [x]) as name:
    ...
    # Do nothing if we know keep_prob == 1
    if tensor_util.constant_value(keep_prob) == 1:
      return x

    noise_shape = noise_shape if noise_shape is not None else array_ops.shape(x)
    # uniform [keep_prob, 1.0 + keep_prob)
    random_tensor = keep_prob
    random_tensor += random_ops.random_uniform(noise_shape,
                                               seed=seed,
                                               dtype=x.dtype)
    # 0. if [keep_prob, 1.0) and 1. if [1.0, 1.0 + keep_prob)
    binary_tensor = math_ops.floor(random_tensor)
    ret = math_ops.div(x, keep_prob) * binary_tensor
    if context.in_graph_mode():
      ret.set_shape(x.get_shape())
    return ret

不同dropout方案对比实验

如果在非dropout阶段不进行scaled会如何？
scaled
scaled.png
without_scaled
without_scaled.png
实验也说明非dropout阶段如果没有进行scaled（求平均），对应的loss会比train阶段高，同时acc也会降低。

桥豆麻袋，到这里好像出现了一点问题：
按照我们上面的思路，在test和evaluate阶段，我们从对sub-model求平均转化为对每个神经元的output进行scaled down，即 $activation(x * W ) * (1 - p)$， 而我们在实现时，只是对x进行scaled up操作，如果后面接的层的激活函数是线性的，这样处理没有什么问题，但是，后面的层不总是线性激活函数，那此时，$output = activation(x * (1-p) * W) != activation(x*W) * (1 - p)$,即我们得到的输出与我们想要的并不一样，按照以上的理解，我们对output进行scaled-down，验证一下两者的区别。
scaled_input
scaled_input.png
scaled_output
scaled_output.png

看上去对output进行scaled-down结果稍微好一点，但是并不显著，此时的激活函数是relu，而且是在倒数第二层，换个激活函数试试。
scaled_input_tanh
scaled_input_tanh.png
scaled_output_tanh
scaled_output_tanh.png
结果看上去对output进行scaled-down效果稍微差一些，但差距不大。
代码地址https://github.com/xv44586/Papers/tree/master/DeepLearning/Dropout，感兴趣的可以试试其他方式。
既然两种方式在结果上看，效果差不多，而对output进行scaled-down需要添加一个AfterDropLayer，逻辑会在不同的层中，而对inputs直接进行scaled-up，所有逻辑都保存在一个layer中，更清晰。
But，Why？为什么两种方式的结果效果差异不大？真让人头秃啊！

论文地址
http://www.jmlr.org/papers/volume15/srivastava14a/srivastava14a.pdf

================================

updating…

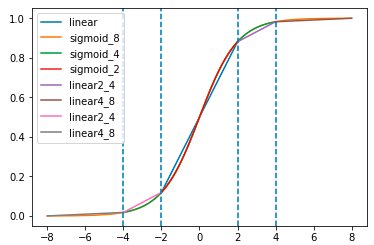
image.png

上图是sigmoid函数在[-8,8]区间的图像，其中linear是由[-8,-4,-2,2,4,8]截断的直线，看图可以看出，sigmoid在区间内都非常的接近”linear”，梯度变化较大的部分只在几个拐点周围，大部分都是近似”linear”,所以也就解释了为什么两种方式有差异，但是差异并不大。

关于头图

大四竞赛作品截图

如果觉得这篇文章不错，对你有帮助，欢迎打赏一杯蜜雪冰城。

logo
Glove模型
深入谈谈word2vec