偏差与方差

偏差 (bias)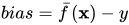

即模型的期望预测与真实值之间的差异。

方差 (variance)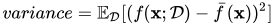

方差通常衡量模型对不同数据集的敏感程度，也可以认为是衡量模型的不稳定性。若方差大，则表示数据的微小变动就能导致学习出的模型产生较大差异，即对应的模型结构风险更高。

有了偏差和方差的定义，我们就能推导出模型的期望泛化误差：

如果我们能在保持bias基本不变时，降低variance，则模型的期望泛化误差降低，从而降低模型过拟合风险。

降低模型过拟合

集成模型

假设我们现在有一个集成模型，其过程为从整体样本中进行采样，得到n份独立且与整体同分布的样本集，然后选择同样的模型进行训练，最后取平均。由于单个模型对应数据同分布，模型相同，则对应的bias和variance相同，而

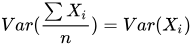
所以最终模型的bias与单模型的bias相同；另一方面，由于各个子模型独立，则

此时可以显著降低模型的variance，根据模型泛化误差期望公式，此时的集成模型的期望泛化误差将小于单模型的期望泛化误差，从而降低了模型的过拟合。

Bagging

针对上述集成模型，当各个子模型相同时，

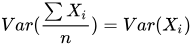
此时不会降低variance。

对应公式：设有n个随机变量，两两变量之间的相关性为𝜌，则方差为

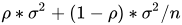
Bagging对样本重采样，对每一重采样得到的子样本集训练一个模型，最后取平均。由于子样本集有相似性，同时也使用同种模型，则各个子模型有相似的bias和variance，由上面结论可知，此时的bias与单模型近似相同，所以bagging不能显著降低bias。（因此在选择模型时，需要选择bias小的模型）子模型介于相同与独立两个极端情况之间，所以对应variance会处于var(x) 与 var(x)/n之间，即通过降低上述公式中的第二项降低整体方差。
而根据模型期望泛化误差公式，由于方差的降低，也能带来最终模型的期望泛化误差的降低，从而降低过拟合。

随机森林

随机森林是一种常用的Bagging模型，其通过对样本进行有放回的采样，构造n个样本集，同时对特征列进行采样后进行模型训练，即同时降低上述公式中的两项，来降低方差，从而降低过拟合。

关于头图

摄于杭州青芝坞

Buy me a coffee

如果觉得这篇文章不错，对你有帮助，欢迎打赏一杯蜜雪冰城。