绪论

在实际应用的机器学习方法里，GradientTree Boosting （GBDT）是一个在很多应用里都很出彩的技术。XGBoost是一套提升树可扩展的机器学习系统。2015年Kaggle发布的29个获胜方法里有17个用了XGBoost。在这些方案里，有8个仅用了XGBoost，另外的大多数用它结合了神经网络。对比来看，第二流行的方法，深度神经网络，只被用了11次。这个系统的成功性也被KDDCup2015所见证了，前十的队伍都用了XGBoost。此外，据胜出的队伍说，很少有别的集成学习方法效果能超过调好参的XGBoost。
主要创新点：

• 设计和构建高度可扩展的端到端提升树系统。
• 提出了一个理论上合理的加权分位数略图（weighted quantile sketch ）来计算候选集。
• 引入了一种新颖的稀疏感知算法用于并行树学习。 令缺失值有默认方向。
• 提出了一个有效的用于核外树形学习的缓存感知块结构。 用缓存加速寻找排序后被打乱的索引的列数据的过程。

算法原理

学习目标

首先来看下我们是如何预测的：
XGBoost是一个树集成模型，他将K（树的个数）个树的结果进行求和，作为最终的预测值。即：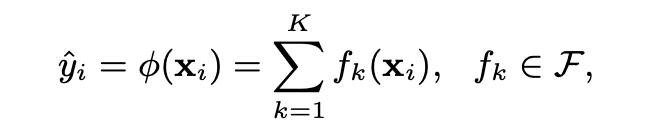

假设给定的样本集有n个样本，m个特征，则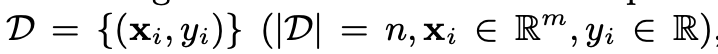

其中 xi 表示第i个样本，yi 表示第i个类别标签，回归树（CART树）的空间F为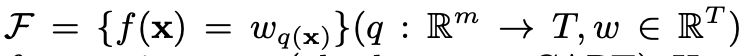

其中q代表每棵树的结构，他将样本映射到对应的叶节点；T是对应树的叶节点个数；f(x)对应树的结构q和叶节点权重w。所以XGBoost的预测值是每棵树对应的叶节点的值的和。
我们的目标是学习这k个树，所以我们最小化下面这个带正则项的目标函数：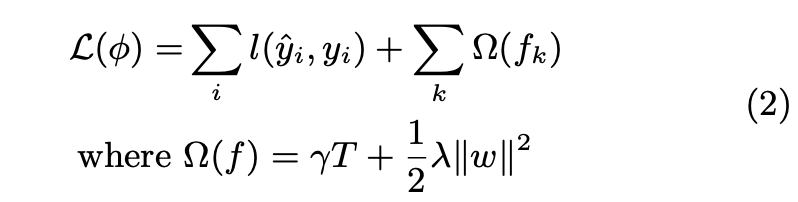


上式的第一项是损失误差，如MSE和logistic等，第二项是正则项，控制树的复杂度，防止过拟合。
式子2中目标函数的优化参数是模型（functions），不能使用传统的优化方法在欧氏空间优化，但是模型在训练时，是一种加法的方式（additive manner），所以在第t轮，我们将f（t）加入模型，最小化下面的目标函数：

训练时，新的一轮加入一个新的f函数，来最大化的降低目标函数，在第t轮，我们的目标函数为 ：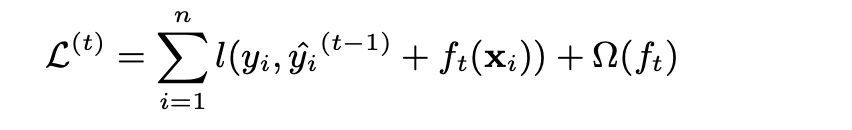

接下来我们将目标函数进行泰勒展开，取前三项，移除高阶小无穷小项，最后我们的目标函数转化为：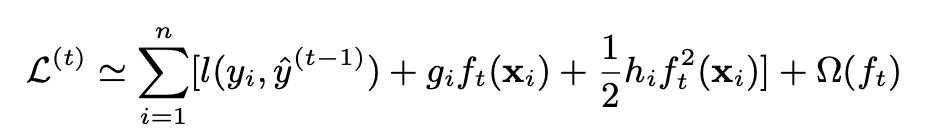

其中：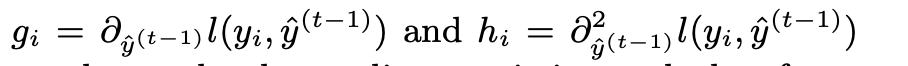

接下来我们求解这个目标函数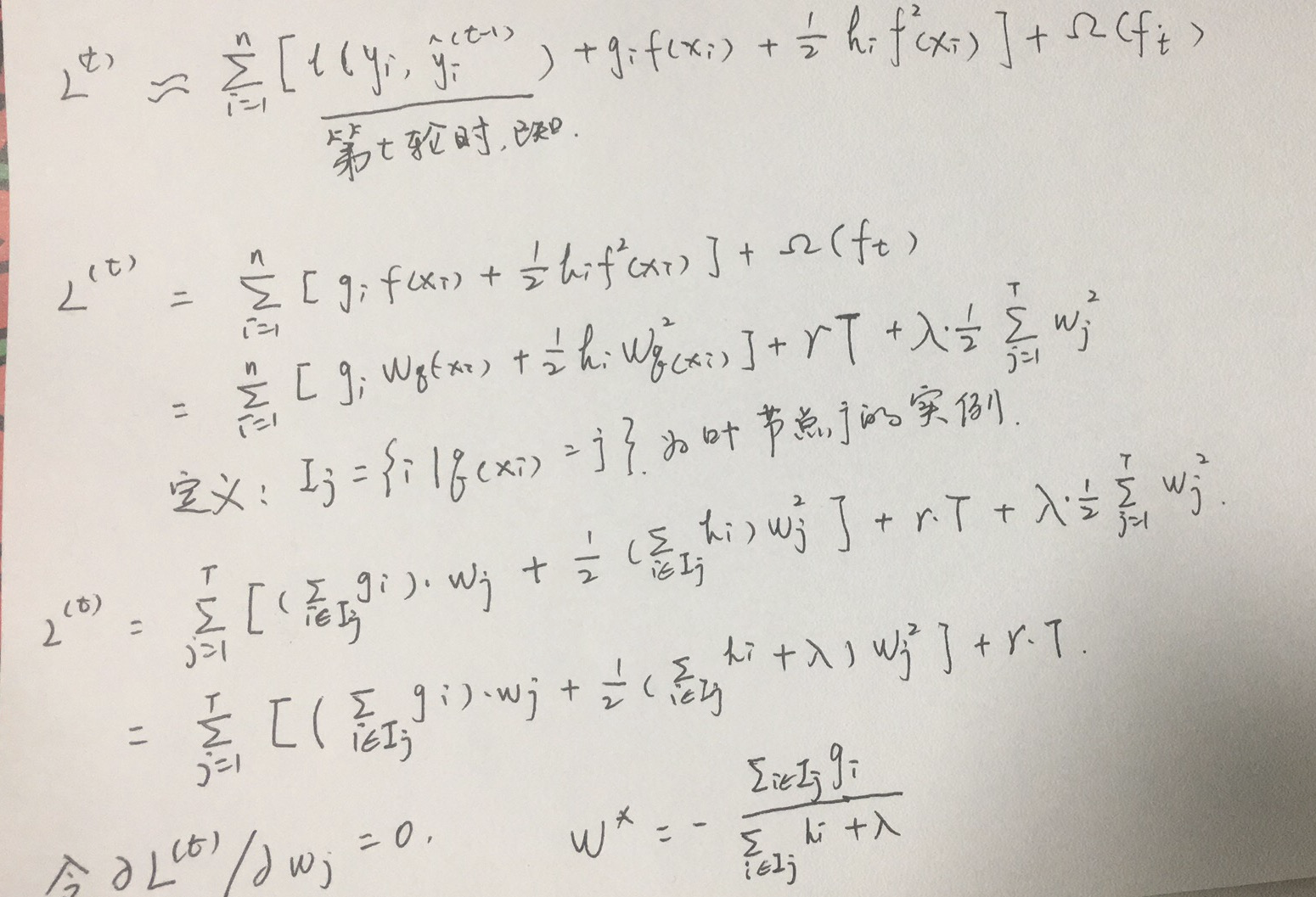

最终我们将关于树模型的迭代转化为关于树的叶子节点的迭代，并求出最优的叶节点分数。将叶节点的最优值带入目标函数，最终目标函数的形式为：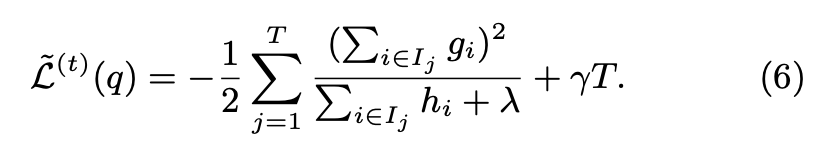

上式可以作为得分函数用来测量树结构q的质量，他类似与决策树的不纯度得分，只是他通过更广泛的目标函数得到

通过上式我们可以看到，当树结构确定时，树的结构得分只与其一阶倒数和二阶倒数有关，得分越小，说明结构越好。

节点划分

而通常情况下，我们无法枚举所有可能的树结构然后选取最优的，所以我们选择用一种贪婪算法来代替：我们从单个叶节点开始，迭代分裂来给树添加节点。节点切分后的损失函数：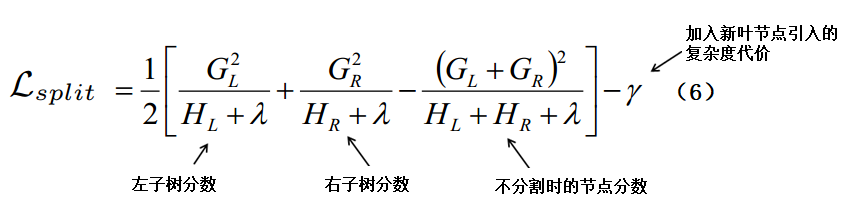

上式用来评估切分后的损失函数，我们的目标是寻找一个特征及对应的值，使得切分后的loss reduction最大。γ除了控制树的复杂度，另一个作用是作为阈值，只有当分裂后的增益大于γ时，才选择分裂，起到了预剪枝的作用。

缩减与列采样

除了在目标函数中引入正则项，为了防止过拟合，XGBoost还引入了缩减(shrinkage)和列抽样（column subsampling），通过在每一步的boosting中引入缩减系数，降低每个树和叶子对结果的影响；列采样是借鉴随机森林中的思想，根据反馈，列采样有时甚至比行抽样效果更好，同时，通过列采样能加速计算。

寻找最佳分割点算法

树模型学习的一个关键问题是如何寻找最优分割点。第一种方法称为基本精确贪心算法（exact greedy algorithm）：枚举所有特征的所有可能划分，寻找最优分割点。该算法要求为连续特征枚举所有可能的切分，这个对计算机要求很高，为了有效做到这一点，XGBoost首先对特征进行排序，然后顺序访问数据，累计loss reduction中的梯度统计量（式6）。

上述方法是一个非常精确的分割点算法，但是当数据无法完全加载进内存或分布式的情况下，该算法就不是特别有效了。为了支持这两种场景，提出了一种近似算法：根据特征分布的百分位数，提出n个候选切分点，然后将样本映射到对应的两个相邻的切分点组成的桶中，聚会统计值，通过聚会后的统计值及推荐分割点，计算最佳分割点。该算法有两种形式：全局近似和局部近似，其差别是全局近似是在生成一棵树之前，对各个特征计算其分位点并划分样本；局部近似是在每个节点进行分裂时采用近似算法。近似算法的流程：

带权重的分位数略图（weighted quantile sketch）算法

在近似算法中重要的一步是寻找候选分割点，通常情况下，特征的百分位数使数据均匀的分布在数据上。现在我们定义一个数据集Dk = {(x1k, h1), (x2k, h2) … }代表样本的第k个特征及其对应的二阶梯度，现在我们定义一个函数rk：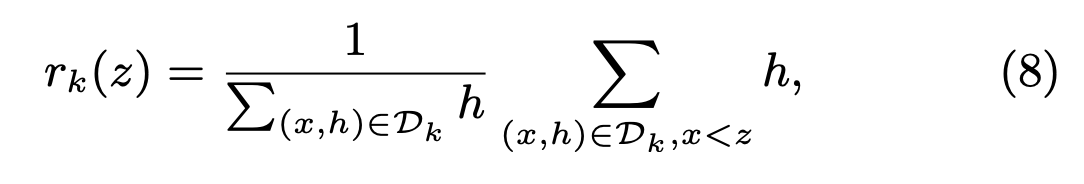

上式代表特征k小于特征z的样本比例，我们的目标是寻找候选分割点{sk1, sk2,…}，使它满足：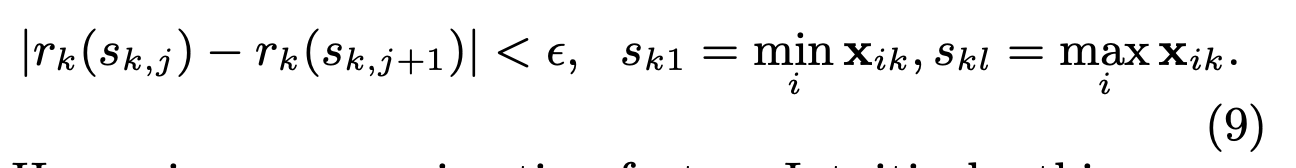

其中e是候选因子，即切分的百分位数，所以最后有大约1/e个候选分割点。那为什么可以用二阶倒数h来代替权重呢？我们将目标函数变形为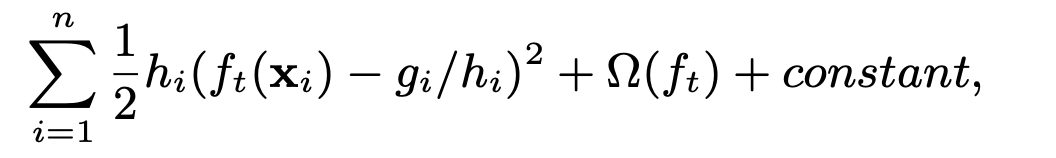

上式可以看成是label是gi/hi，权重是hi的平方损失，这对于大数据下寻找划分点非常重要。在以往的分位法中，没有考虑权值，许多存在的近似方法中，或者通过排序或者通过启发式方法（没有理论保证）划分。文章的贡献是提供了理论保证的分布式加权分位法。
为什么要对目标函数进行类似的变形？思考一下我们划分分割点的目标是什么？是希望均匀的划分loss，而不同样本对loss的权重不同，不考虑权重直接按样本划分时，loss的分布是不均匀的，对应的分位点就会有偏差。
PS：文章中的近似变形感觉不太近似，更近似的变形可能是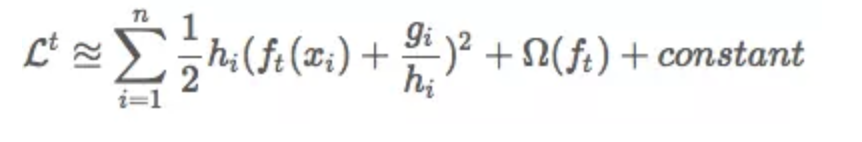
即label是-gi/hi的带权重平方损失。不知道文章内为啥是另一种形式

稀疏自适应分割策略

实际情况下避免不了数据稀疏，产生数据稀疏的原因主要有三个：1，数据缺失，2，统计上为0，3，one-hot编码。而适应稀疏数据非常重要。XGBoost提出的是在计算分割后的分数时，遇到缺失值，分别将缺失值带入左右两个分割节点，然后取最大值的方向为其默认方向。

以上就是XGBoost所涉及的算法原理。

XGBoost的优缺点

与GBDT对比

• 1.GBDT的基分类器只支持CART树，而XGBoost支持线性分类器，此时相当于带有L1和L2正则项的逻辑回归（分类问题）和线性回归（回归问题）。
• 2.GBDT在优化时只使用了一阶倒数，而XGBoost对目标函数进行二阶泰勒展开，此外，XGBoost支持自定义损失函数，只要损失函数二阶可导
• 3.XGBoost借鉴随机森林算法，支持列抽样和行抽样，这样即能降低过拟合风险，又能降低计算。
• 4.XGBoost在目标函数中引入了正则项，正则项包括叶节点的个数及叶节点的输出值的L2范数。通过约束树结构，降低模型方差，防止过拟合。
• 5.XGBoost对缺失值不敏感，能自动学习其分裂方向
• 6.XGBoost在每一步中引入缩减因子，降低单颗树对结果的影响，让后续模型有更大的优化空间，进一步防止过拟合。
• 7.XGBoost在训练之前，对数据预先进行排序并保存为block，后续迭代中重复使用，减少计算，同时在计算分割点时，可以并行计算
• 8.可并行的近似直方图算法，树结点在进行分裂时，需要计算每个节点的增益，若数据量较大，对所有节点的特征进行排序，遍历的得到最优分割点，这种贪心法异常耗时，这时引进近似直方图算法，用于生成高效的分割点，即用分裂后的某种值减去分裂前的某种值，获得增益，为了限制树的增长，引入阈值，当增益大于阈值时，进行分裂；

与LightGBM对比

• 1.XGBoost采用预排序，在迭代之前，对结点的特征做预排序，遍历选择最优分割点，数据量大时，贪心法耗时，LightGBM方法采用histogram算法，占用的内存低，数据分割的复杂度更低，但是不能找到最精确的数据分割点。同时，不精确的分割点可以认为是降低过拟合的一种手段。
• 2.LightGBM借鉴Adaboost的思想，对样本基于梯度采样，然后计算增益，降低了计算
• 3.LightGBM对列进行合并，降低了计算
• 4.XGBoost采样level-wise策略进行决策树的生成，同时分裂同一层的节点，采用多线程优化，不容易过拟合，但有些节点分裂增益非常小，没必要进行分割，这就带来了一些不必要的计算；LightGBM采样leaf-wise策略进行树的生成，每次都选择在当前叶子节点中增益最大的节点进行分裂，如此迭代，但是这样容易产生深度很深的树，产生过拟合，所以增加了最大深度的限制，来保证高效的同时防止过拟合。

参考：https://arxiv.org/pdf/1603.02754.pdf
https://www.zhihu.com/question/41354392/answer/98658997

关于头图

风格迁移模型效果图

Buy me a coffee

如果觉得这篇文章不错，对你有帮助，欢迎打赏一杯蜜雪冰城。