最大熵是概论模型学习的一个准则。

逻辑回归

逻辑回归分布：

对于连续随机变量X，X服从逻辑回归分布是指X具有以下分布函数和密度函数：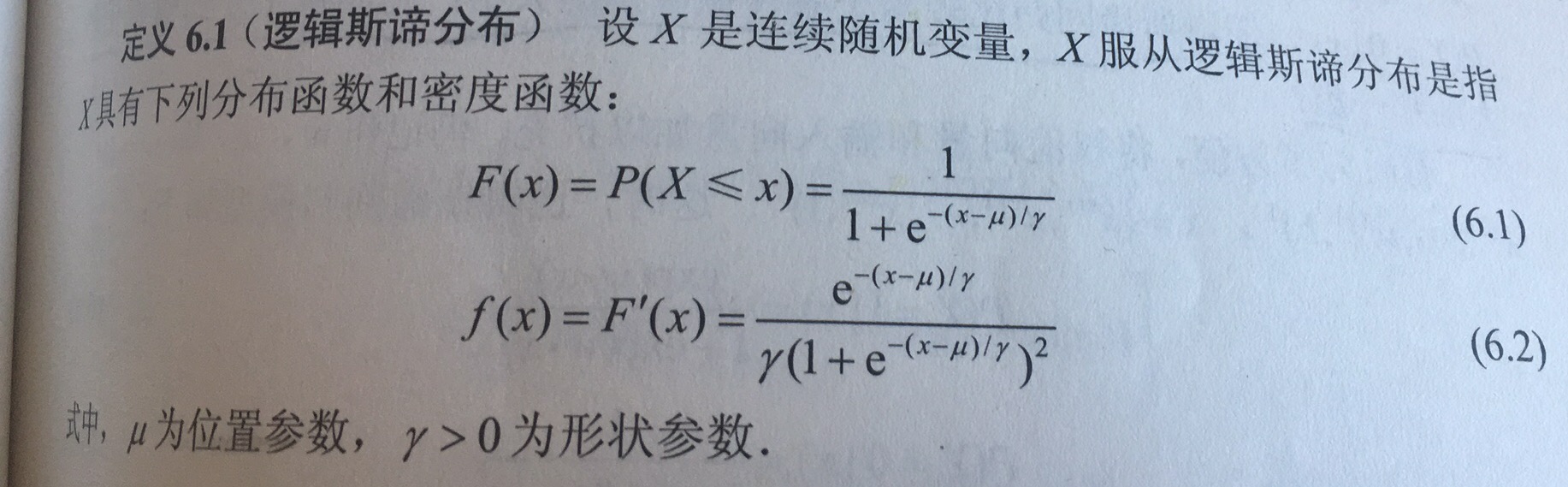

二项逻辑回归模型：

二项逻辑回归是一种分类模型，由条件概论分布P(Y|X)表示，其中Y取值为0或1，其条件概论分布为：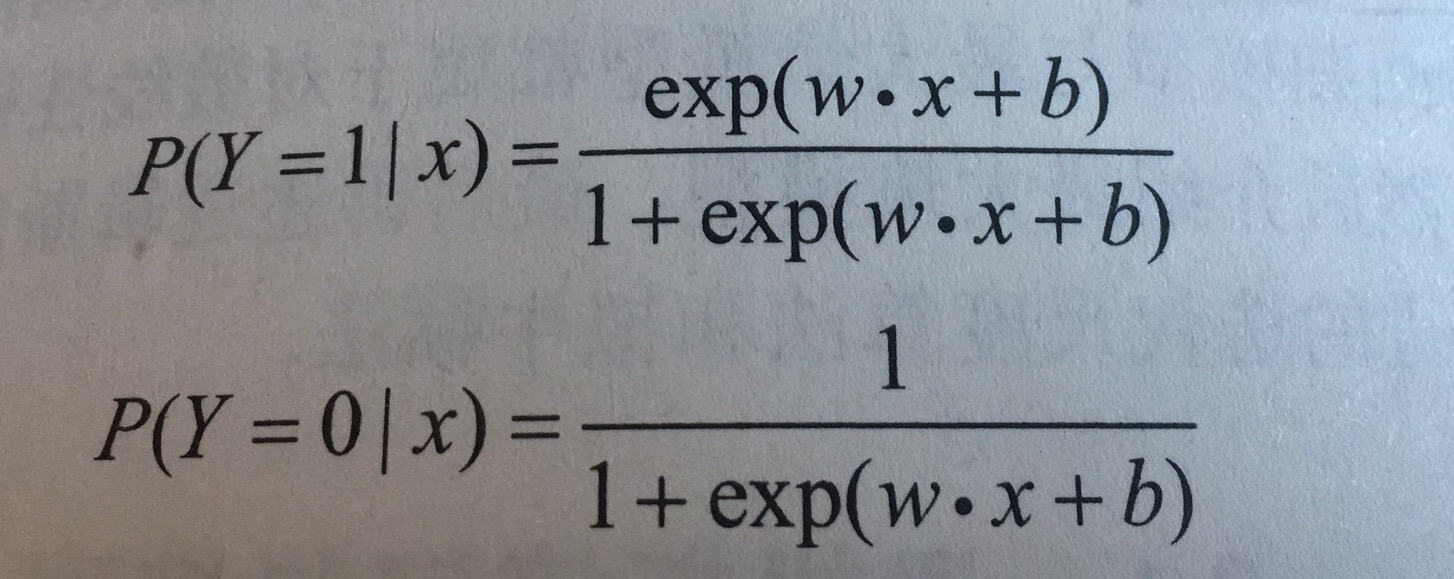

对于给定的输入x，可以求出P(Y=1|x)和 P(Y=0|x)，逻辑回归通过比较两个条件概率的大小，将x分到概率值大的类中。

逻辑回归模型特点：

一个事件的几率（odds）是指该事件发生与不发生的概率比值，如果事件发生的概率是p，则几率为p/(1-p)，其对数几率或logit函数是logit(p) = log(p/1-p)，对逻辑回归而言:
$log(P(Y=1|x)/(1-P(Y=1|x)) = wx$
即输出Y=1的对数几率是x的线性函数。

最大熵模型

熵

假设离散随机变量X的概率分布是P(X),其熵为：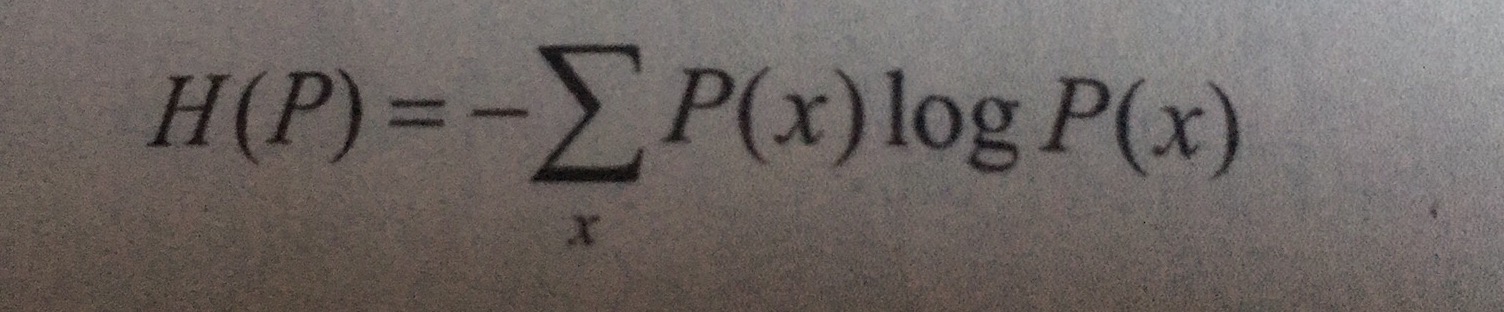

熵满足下列不等式：
$0<=H(P)<=log|X|$
其中|X|指X的取值个数，当且仅当X当分布是均匀分布时，右边等号成立，即均匀分布时，熵最大。
最大熵原理是概率模型学习的一个准则，其认为在学习概率模型时，熵最大的模型是最好的。直观地说，即在选择概率模型时，首先要满足已有的事实，在没有更多信息的情况下，那些不确定的部分是“等可能的”，“等可能”不容易操作，而熵则是一个可以优化的数值指标，通过最大化熵来表示等可能。
举例说明，当没有给任何多余信息时，我们猜测抛掷硬币时，每面朝上的概率都是0.5，仍骰子时，每面朝上的概率都是1/6，即没有额外信息时，认为都是等可能是“最合理”。假如有一枚骰子，扔出1和4的概率之和是1/2，则此时我们认为1和4朝上的概率是1/4，而其余四面朝上的概率是1/8，即首先要满足已知信息，没有额外信息时，均匀分布“最合理”。

最大熵模型：

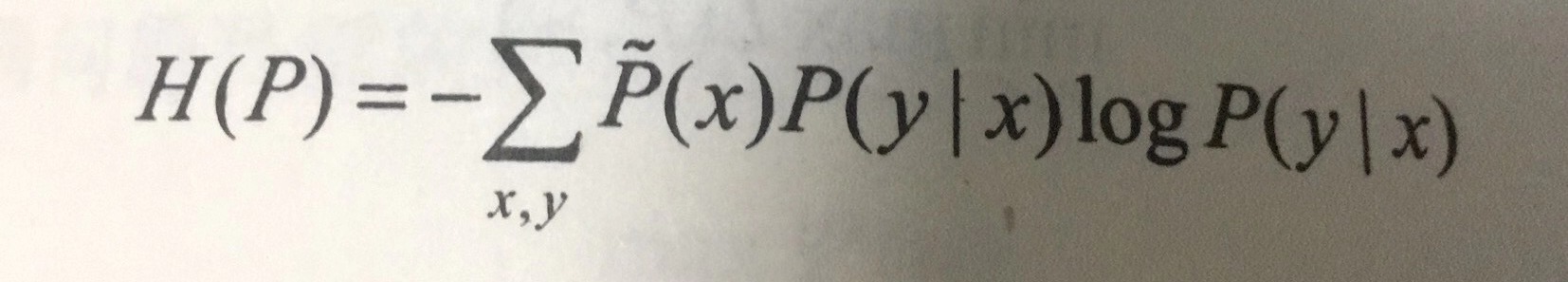
其中条件熵最大的模型称为最大熵模型

模型学习：

最大熵模型的学习可以形式化为约束最优化问题。通过引入拉格朗日乘子将约束最优化问题转化为无约束最优化的对偶问题。

PS：
西瓜书上认为对于任意单调可微函数g(),令
$(y) = wx + b$
这样的模型称为广义线性模型，其中函数g为联系函数。对于二分类任务，其输出为0或1，而线性模型的输出为实数域，需要一个函数将实数域的输出转化到0/1值，最理想的函数是单位阶跃函数，即大于0输出1，小于0输出0，等于0输出0.5，但是该函数不连续，不能用作g(),所以使用sigmoid函数替代。
逻辑回归有很多优点，如直接对分类可能性进行建模，无需事先假设数据分布，不仅预测出类别，而是得到近似概率预测。

统计学习方法中给出逻辑回归分布函数，通过引入最大熵模型，求解模型；西瓜书中通过广义线性模型，将sigmoid函数作为连续函数g给出罗辑回归模型，并说明罗辑回归不需要事先假设数据分布。两者都没有明确说明为什么是sigmoid函数，而答案在http://www.win-vector.com/dfiles/LogisticRegressionMaxEnt.pdf 可以看到，感兴趣的可以读读。

关于头图

摄于奥森

Buy me a coffee

如果觉得这篇文章不错，对你有帮助，欢迎打赏一杯蜜雪冰城。